波浪能量与波能传递：船舶运动理论

两端伸展到无限远处的平面前进波的总能量是无限的，本节考察的是单位宽度的一个波长内波浪的能量。

自由水面由于产生波形而使位能增加。如图3.8所示，体积微元d x d z（单位宽度上）中流体的重力位能是ρgz d x d z。故一个波长的重力位能E g为

图3.7　波浪质点的运动轨迹

（a）极浅水；（b）浅水；（c）深水

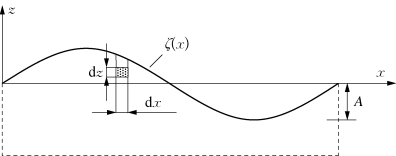
图3.8　一个波长中波浪的能量

式中，ζ=A ei（mx-ωt）为波面位移。因积分号中出现非线性的平方运算，如前文所述，应先取实部然后运算。这样就有

另外，流场中由于流体质点的运动而具有动能。单位宽度的波浪动能为

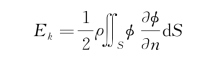
式中，S为如图3.8所示的虚线面（两侧虚线面相距恰为一个波长）和波面。在底面，无论在有限深水的池底或无限深水情况中无穷深处的某一假面水平面上，均有∂φ／∂n=-∂φ／∂z=c。在两侧面上，由于运动的周期性，相应点上φ值相同，∂φ／∂n的数值也相同，而法线方向正好相反，因此两侧面对积分的贡献之和等于零。最后只剩在波面上的积分。在线性化的前提下，波面的积分边界近似地取在z=0上，所以

将式（3.17）取实部代入积分，再利用色散关系式（3.14），得到

如果不计表面张力，则波浪总能量即为重力位能与动能之和。总能量为

然而在有表面张力存在的情况下，自由面形状的变化不仅改变了质量的垂向分布，改变了重力位能，而且还抵抗表面张力做功。这部分能量也以位能的形式贮存在流体中，称张力位能，记为E t。

如图3.9所示，原来在静水面上的d x微段变形后为

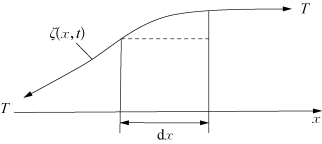
图3.9　静水面的变形伸长

其实际伸长为

所以张力位能当为(www.xing528.com)

一个波长内的张力位能E t为

总位能为

一个波长内的总能量就是

由此可见，无论计入或不计入表面张力，均有

在平面前进波中，一个波长内的动能和位能都不随时间而变。事实上，平面前进波的波形在传播过程中是不随时间变化的，所以位能不变，按总能量守恒，动能也就不变。

波浪传播过程中能量也在转移。现以无限深水中的平面前进波为例加以讨论。讨论中不计入表面张力。

任取一垂直于波浪传播方向的平面A（见图3.8），A在oy方向仍取单位宽度，计算在一个波浪周期中有多少能量流过A面。转移的能量可以看作是作用在A面上的压力在一个波浪周期内做的功。在A面上取一面积微元d z，在d t时间内压力在面源d z上做功：

式中，p-为作用于A面上的压力，u为A面上水质点的水平速度。

按式（3.22），无限深水中平面前进波的速度势为

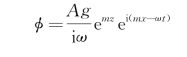
注意到ω2=gm，故有

由拉格朗日积分式（1.9），压力是

因此在一个周期内波浪在整个平面A上所做的功为

比较式（3.37）与式（3.32）易知，能量传播为波浪总能量的一半；也就是说，在波浪传播过程中，总能量的一半随波前进，而另一半则留在后方。实际上，由于质点的轨迹是条封闭曲线，动能不变，故只有位能传向前去。

单位时间内所做功的平均值是

这里引入了一个新的速度c g=0.5c。由式（3.32）知，0.5ρg A 2表示单位波长的波浪总能量，或谓一个波长内的能量平均值或平均能量密度。显然c g表征了能量传播的速度，它等于波速（或称相速）的一半，该能量传播速度等于波速群。无限深水重力波，对其他类型的线性水波也有同样的结论，当然它们的能量传播速度或群速不一定恰好为相速度的二分之一。