平面前进波及波浪特性

波浪是具有自由表面的流体的一种重要运动形态，本节将讨论其中一个特殊的波动形式，即均匀水深的一维的平面前进波。

取坐标系如图3.4所示，坐标原点位于静水面上，水深均匀为H，有波动时液面坐标为z=ζ（x，t），并假定波高与波长相比为小量。如前一章所述，水视为理想、不可压缩的均匀流体，流动是无旋的。这时，流场中存在着速度势φ（x，z，t）。根据连续性要求，速度势满足拉普拉斯方程

图3.4　平面前进波

边界条件应包括自由面条件和物面条件（现在即池底条件）。在小波高的假定下，自由面条件可以线性化，并认为这一边界条件近似地在未扰静水面z=0上得到满足。由式（2.23），自由面条件可记为

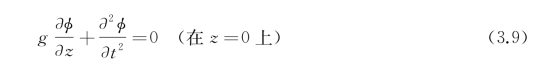
式中，g是重力加速度。池底条件z=-H时，有

除此之外，一个定解问题还需给出无限远方（辐射条件）和初始条件。本节研究的是平面前进波，故波在传播过程中波高不变。进而我们假定波动从左向右传播，并已传播了一个相当长的时间，波浪运动已达稳态，波形是规则的。如前面所述，这个假定相当于给出了初始条件。由式（2.26）可见辐射条件可写作

这里m和ω为表征波浪的特征量，它们的含义将在下文中讨论。

拉普拉斯方程式（3.8）与边界条件式（3.9）、（3.10）及（3.11）构成了完整的定解问题。

从上节中分离变量求解式（3.7）知，其中第一和第三式不能形成正弦波，故可供选择的解为

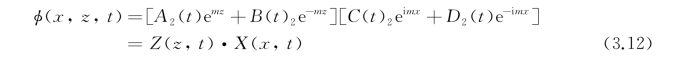
它满足拉普拉斯方程，式中出现的t的任意函数则须由边界条件来确定。

速度势φ（x，z，t）须满足池底条件（3.10），显然，这只与解中的Z（z，t）项有关，就是

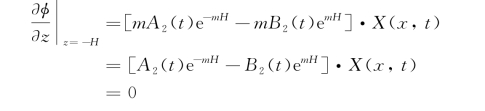
这里既然A 2，B 2为任意的t的函数，故m可被吸收进去。

若令A 2（t）=0.5·α（t）e mH，B 2（t）=0.5·α（t）e-mH，则上式得到满足，其中α（t）为一任意的t的函数。代入式（3.12）即得

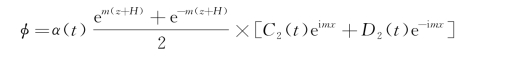
这里α（t）同样可归并进C 2和D 2之中，故

再将上式代入自由面条件式（3.9），有

式中，C··2和D··

2代表函数对时间t的二阶导数。引进色散关系

式中，m和ω为波的两个特征量，H为水深，g为重力加速度。式（3.14）可变成

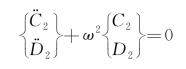
这两个常微分方程的通解分别为

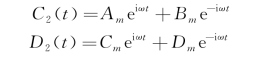
式中，A m、B m、C m和D m是任意常数。

将其代入式（3.13），得到满足池底条件和自由面条件的速度势表达式为

式中，A m和D m项不满足辐射条件，它们代表左传波。而另两项在取实部时是等价的，可任取一项，例如B m项，这样平面右传进行波速度势的最终形式为

有了波浪运动速度势以后，接下来考察平面前进波的性质和一些特征量的含义。　

1）波形ζ（x，t）

设规则波波形具有与速度势相同的振荡因子ei（mx-ωt），即设波形

式中，A为波幅，现在来确定波幅与速度势中常数B m的关系。自由表面上的动力学条件是在z=0上有

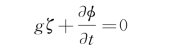
将速度势表达式（3.15）及波形（3.16）代入上式得

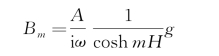
注意到色散关系式（3.14），B m也可记作

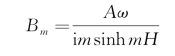
于是速度势φ（x，z，t）可记作

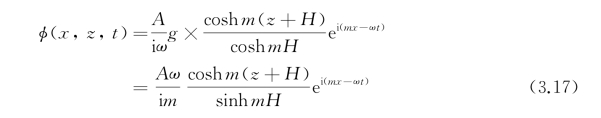
由此可见，速度势在z方向的变化不是正弦型，而是双曲余弦型或指数型的。

在波形和速度势表达式中，令

(www.xing528.com)

θ为相位角，它决定了波形上某点于某一时刻在波峰和波谷间的位置。其中x为所选坐标中的位置量。θ为常数，形成的面称为相位面。在平面波中，相位面是平行平面（垂直于纸面）。θ在空间的梯度即为m，定义m为波数。它的大小等于在波浪传播方向上每2π距离上波峰的平均数目，即m=2π／λ。类似地，定义-∂θ／∂t=ω为波浪振荡的圆频率，它表示每2π时间中过某一定点的波峰的平均数目，即ω=2π／τ。这里λ为波长，τ为波浪周期。

对于θ等于常数的某一相位面。它与波浪峰谷之间的相对位置不随时间变化，即

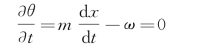
但描述相位面在空间的位置的x却是变化的，它对时间的导数表征了相位面移动的速度，定义为波速或相速c，所以

ω与m满足色散关系式（3.14），因而色散关系也可写作

波速为

重力波的两种极限状态如下。

深水重力波：m H→∞，tanh m H→1，波浪频率和波速分别为

而且cosh m（z+H）／cosh m H→e mz，故速度势表达式（3.17）变成

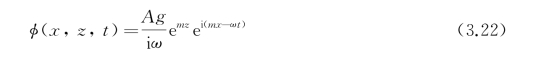
浅水重力波：此时m H→0，tanh m H→m H。波浪频率和波速分别为

而且cosh m（z+H）／cosh m H→1，速度势变成

式中，因子z不复出现，可见在浅水极限状况中，流体质点的水平速度与z无关，且垂向速度为零。

通常认为，当λ＜2H时是深水波；λ＞14H时是浅水波；当2H≤λ≤14H时为有限深水波。

2）流体质点的运动

根据速度势可进而考察流场中水质点的运动。质点的水平速度为

垂向速度为

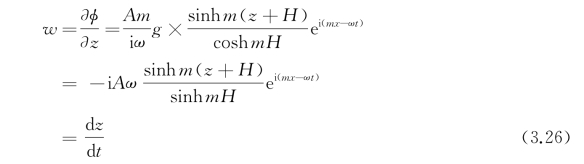
注意到因子-i=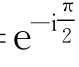，可见在正弦波的情况下，两个速度分量都是简谐振荡，相位差为90°，即垂向速度滞后于水平速度90°。两个速度分量的振幅一般不相同，一个与cosh m（z+H）成比例，另一个与sinh m（z+H）成比例。

由两个函数的曲线（见图3.5）及性质可知：

（1）对某一固定深度（z固定）上的质点，当m H很大时cosh m（z+H）值与sinh m（z+H）值越来越接近。m H→∞时两值相等，故在无限深水中，水平与垂直两个速度分量的振幅是一样的。

（2）水深有限时，sinh m（z+H）＜cosh m（z+H），说明垂向速度振幅比水平振幅小。随着m H的减小，sinh m（z+H）值迅速减小，以零为终值；cosh m（z+H）则减小得比较缓慢，以1为终值。

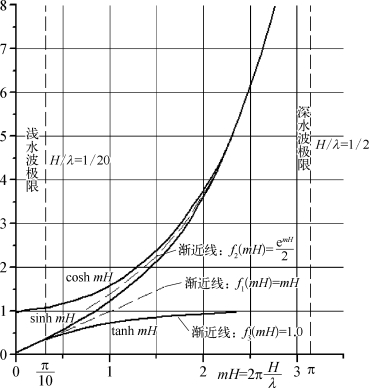
图3.5　双曲函数及渐近线

（3）若取速度分量的实部，容易证明

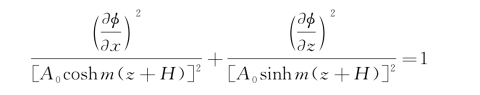
式中，

由式（3.25）和式（3.26）易知，水平速度在波峰与波谷处达最大值，但方向相反；垂直速度则在节点处（ζ=0）达最大值，在池底处z=-H，垂直速度为零。图3.6为波浪速度场一个图例。在无限深水中，随着水深的增加，水质点的水平速度和垂直速度均趋于零。

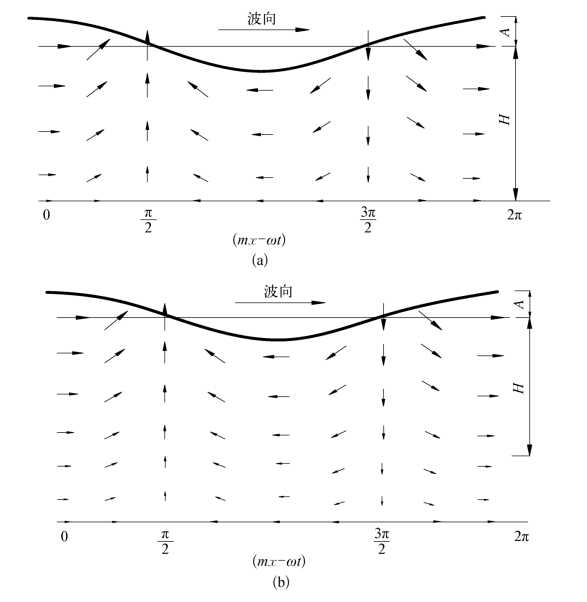
图3.6　进行波的速度场

（a）浅水进行波速度场；（b）深水进行波速度场

由式（3.25）和（3.26）也可求得流体质点的运动轨迹。设某流体质点的平衡位置为（x 0，y 0），x′、z′为质点偏离其平衡位置的位移分量，则质点在某一瞬时的位置为

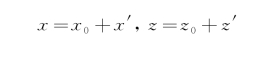
则

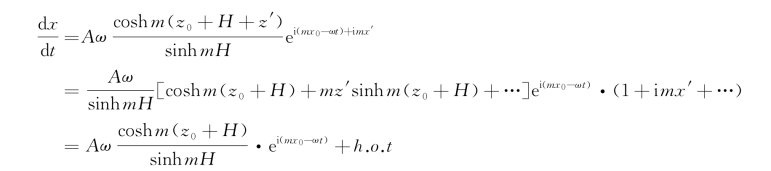
式中，h.o.t代表高阶项。对微幅波而言，质点偏离平衡位置的位移是个小量，高阶项可予忽略。积分上式，就得

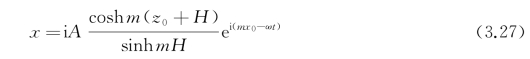
同理可得

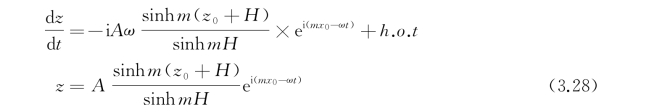
取x与z的实部，并平方相加，经整理即得到质点运动的轨迹方程为

其中：

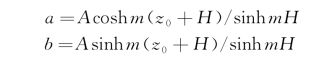
上式为椭圆的一般方程，长轴为2a，短轴为2b。可见流体质点在平均位置（x 0，y 0）附近沿椭圆轨迹作周期运动。水深有限时，在池底z=-H，运动轨迹退化为一水平直线段，即池底上的水质点仅作水平振荡运动。当水深无限（H→∞）时，cosh m（z 0+H）／sinh m H～sinh m（z 0+H）／sinh m H～e mz0椭圆退化为圆，半径为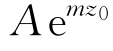，随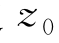按指数规律衰减。不同水深时流体质点的运动轨迹如图3.7所示。