斯托克斯公式与波浪上的船舶运动

设有一光滑曲面S，其边界为光滑曲线C，n为曲面S的单位外法线矢量，如图2.5所示。函数P（x，y，z）、Q（x，y，z）、R（x，y，z）在曲面S及曲线C上具有对x、y、z的一阶连续偏导数。

图2.5　光滑曲面

式中，cos（n，x）为n与ox轴夹角的余弦。

若给定矢量函数V=｛P，Q，R｝，将式（2.56）的三式相加，得

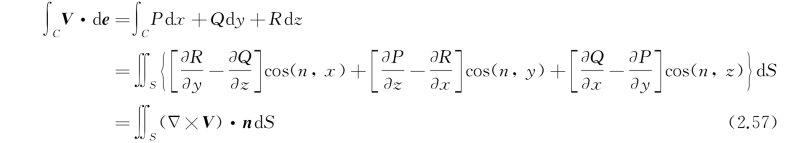
式中，d e=（d x，d y，d z）是曲线C上的微段矢量，n=｛cos（n，x），cos（n，y），cos（n，z）｝，而

式（2.57）是斯托克斯公式的基本形式。从流体力学角度而言，线积分代表沿曲线C的环量（circulation），面积分意味着从曲面S流出的涡量（vorticity），这两者是相等的。上述公式中并未对曲面S作具体规定，故对任何以曲线C为边界且遵守光滑性条件的上述关系恒成立。它的物理意义是，流过上述各曲面（以C为边界）的涡量相等，这也是一种守恒定理。斯托克斯公式还有若干推广形式，下面分别推导。

1）第一斯托克斯公式

在式（2.56）中取P=iφ，Q=jφ，R=kφ（φ为x、y、z的标量函数），将三者相加，得

式（2.58）称为推广的第一斯托克斯公式。

2）第二斯托克斯公式

给定矢量V=（P，Q，R）≡（v 1，v 2，v 3），考察线积分

应用式（2.56），可得

现在i分量积分核中加上和减去一项，j积分核中加上和减去一项，k分量积分核中加上和减去一项，并加以归并整理，右端积分号内核函数分别为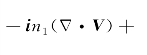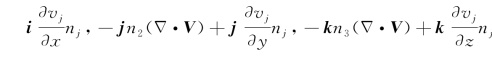，从而上式变成

(www.xing528.com)

如果注意到

则又可得

式（2.59）或（2.60）称为推广的第二斯托克斯公式。

3）第三斯托克斯公式

给定矢量V=（v 1，v 2，v 3），r=（x 1，x 2，x 3），考察积分

展开后上述积分的i方向分量为

应用公式（2.50）后，I 1变成

在右端被积函数中加上和减去项和，并重新整理之，有

式中，

下标i指i方向分量。与式（2.61）对应的其他两个分量可按置换x→y→z→x的法则获得。按I 1i+I 2j+I 3k给出

式中，，若在（2.61）中作不同的组合，还可以证明

式（2.62）和式（2.63）可称作推广的第三斯托克斯公式。