单层势与双层势的关联

单层势和双层势或可分别称为源分布和偶分布。本节主要讨论外部流动问题。如图2.3所示，有一物体处于流场中，物面记为S，外部流域为τe，物面单位内法线矢量为n i，对流域而言，n e为外法线单位矢量。外域中速度势φe，按式（2.41）可表达为

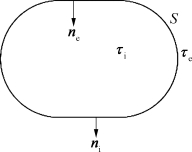
图2.3　流域的定义

闭曲面S内部对目前的问题来说是没有定义的，但我们可在物体内部虚构一个流场，记为τi，边界面上的单位法线矢量n i的方向恰与n e相反，对各自的流域而言都是外法线。内部流场的速度势φi可记为

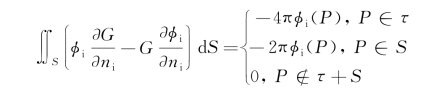
也就是

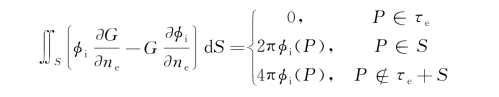
将上式按不同的P点位置的表达式分别减去式（2.43），得

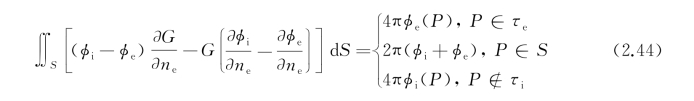
以上的做法，在数学上称为“开拓”。既然内域τi是虚构的，自然带有某种任意性。

1）单层势(www.xing528.com)

若令在S上有φi=φe，并记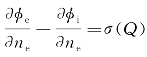，则上式变为

上式左端为含参数P（x，y，z）的积分，它相当于在S上密度为σ（Q）的源分布在场内某点P引起的速度势，称为单层势。显然，这样的势函数在S两边是连续的，其法向导数则不连续。正是其法向导数的阶跃构成了源的强度分布密度σ（Q）。因此，若在表面S上分布源点，内域、外域的势函数都已经确定，在边界曲面上就是源势本身φS（P）。式（2.45）可进而记作

它无论对外部流场、内部流场或边界上的点都是成立的。合适的源强分布σ（Q）应由边界条件决定。

2）双层势

除了上述的选择外，另一种可能的选择是在边界面S上，令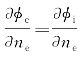，且记m=φi-φe，由式（2.44）有

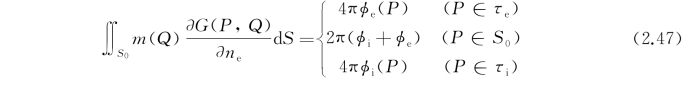
显然，上式的积分核内可视为一偶极子，其偶极矩方向为物面S的法线方向，m（Q）可视作是偶极子分布密度。式（2.47）左端的积分可理解为在S上的密度为m（Q）的偶极子分布在场内某点P上产生的速度势，由于偶极子可认为是放置得极为靠近的源点和汇点所组成，而奇点强度与其距离的乘积保持常数，所以它的面分布就好像是由一层源分布与一层无限靠近的汇分布所组成，故称双层势。容易看出，双层势也是含参变量P的广义积分，在P=Q点上积分核有1／r 2的奇性，比单层势高一阶。尽管如此，还是可以证明在S上的广义积分是存在的，其值等于2π（φi+φe）；然而在S上势函数并不连续，其阶跃值为φi-φe=m。从如图2.4所示的物理直观中容易理解，在偶的分布面中，法向速度在越过边界曲面时是连续的。

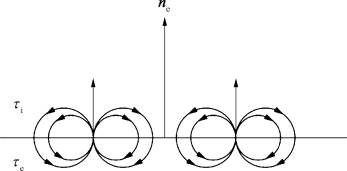
图2.4　偶分布