船舶在波浪上的运动理论中的格林公式

船舶在波浪上运动的流体动力问题关键在于求解流场中的速度势，即求解在确定的边界条件下的拉普拉斯方程。目前，关于拉普拉斯方程边值问题的求解已有许多成熟的方法，对这些方法的介绍和讨论已超出本书的范围，有兴趣的读者可参考文献［31］。在本书中，主要采用格林函数法（Green's function method）来处理速度势的求解问题。

格林函数法又称奇点分布法（singularity distribution method）、边界积分方程法或边界单元法（boundary element method）。这种方法在应用上相当灵活，对边界的适应性较强，格林函数法的理论和数学基础早为人所知，在数学上亦有许多研究。但由于这一方法的基本特点是把边值问题变换成积分方程求解，一般不大容易获得解析解，其本质上属于一种数值方法，计算工作量相当大，直至20世纪60年代初期，随着高速大容量电子计算机的出现和迅速发展，这一方法才获得进一步的发展和完善，并开始在工程实际中广泛地应用。目前，在连续介质力学的许多领域内，都可见到这一方法的有效应用。

格林函数法的基础是格林公式，它们可由高斯公式（或谓散度定理）推导得到。对三维空间中的有界区域τ，有关系式：

式中，S是体积τ的充分光滑的边界面；n为曲面S的单位外法线矢量（从流体域指向外部），矢量A在闭区域τ+S上连续，在τ内有连续偏导数的任意矢量函数。

现令，于是

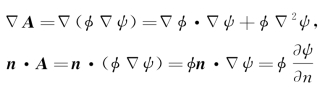
由散度定理（2.29）得

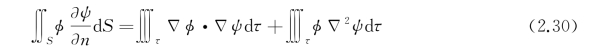
这是格林第一公式。

同理若令，则有类似的表达式：

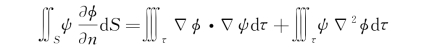
它与式（2.30）之差给出格林第二公式：

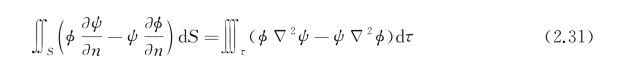
格林第二公式在τ内二阶连续可微，在τ+S上有一阶连续偏导数的任意函数φ（x，y，z）和ψ（x，y，z）成立。作为推论，若φ和ψ在域τ内处处调和，即在τ内处处满足0，则

式（2.32）在本书中将一再用到，在本书中也称它为格林第二公式。

现设φ（x，y，z）为待求的速度势，它是一个调和函数，满足Δ2φ=0；如果能够恰当地选择函数ψ，使得式（2.31）的右端为

式中，P（x，y，z）为域内任一场点，Q（ξ，η，ζ）为域内变点，那么，势函数φ在域内任一点P上的值即可由它在边界上的函数值和法向导数值来确定。

可以证明，具有这种性质的ψ必然满足

式中，δ（P-Q）是狄拉克（Dirac）δ函数（一种广义函数），以一维情况为例，这个函数有性质

式（2.33）是个泊松（Poisson）方程，它的一个特解是源函数：

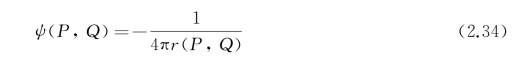
式中，r（P，Q）为P与Q之间的距离，即。函数ψ表示在Q点放置的单位强度点源在P点诱导的速度势，而∂ψ／∂n则表示极矩在n方向的单位偶极子诱导的速度势。ψ（P，Q）除P=Q点外处处满足Δ2ψ=0。

现在研究域的内部问题。设场点P（x，y，z）处在闭区域τ+S内，如图2.1（a）所示。在P点上ψ有奇性。现环绕场点作一半径为rε的小球，小球的表面积设为Sε，于是，在S+Sε所围的区域中处处都有Δ2ψ=0。

应用格林第二公式（2.32）可得

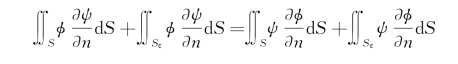
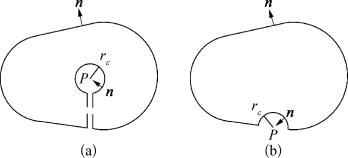
图2.1　格林公式的积分表面(https://www.xing528.com)

（a）场点P处在闭区域τ+S内；（b）场点P处在边界上

在Sε上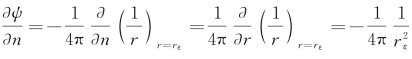，，利用中值定理，有

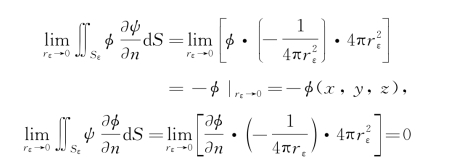
因此得到

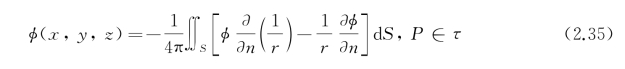
考察上式可知，既然代表空间偶极子，则表面S上代表空间点源，和φ值分别相当于源强和偶强的分布密度。上式表明域内某一点的势函数可以由表面的奇点分布来表示。

如果场点落在边界上，如图2.1（b）所示，绕场点作一半径为rε的小球，按上文同样的证法可以得到

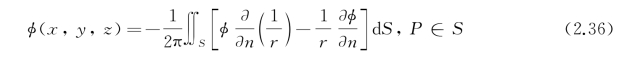
式（2.36）是对光滑边界推导得到的，如果边界上有曲面导数不连续的点，且场点就在该点上，则式（2.36）中系数1／2π应改为1／α，α为该点上曲面所张的立体角。

如果场点在区域τ+S的外面，由式（2.31）得

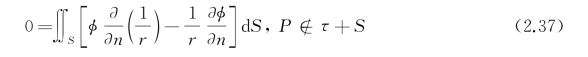
综上所述，对于内域问题，按场点位置的不同分别有如下表达式：

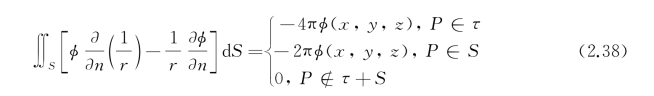
式（2.38）称为格林第三公式。

如果研究的是闭曲面S以外的外域流动问题，则域的边界面可认为是S+S∞，S∞为外部假想球面（控制面），半径R→∞（见图2.2）。在S∞上有

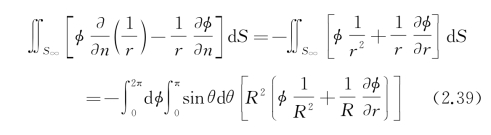
如果当R→∞时，φ满足：

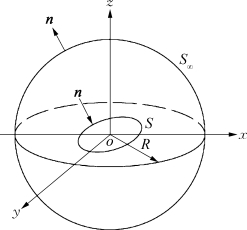
图2.2　外域边界

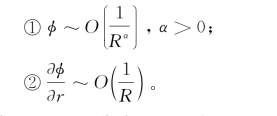
则S∞上的积分式（2.39）在R→∞时趋于零。这时格林第三公式仍然成立，其形式与式（2.38）完全一样，但这时S上的法线取向与内部问题相反。给定S上的奇点分布，场中任意点P的速度势φ（x，y，z）即可按此确定。

前面已经指出只是泊松方程的一个特解，因此ψ形式不是唯一的。事实上，如果存在域τ内处处调和的函数G*（P，Q），则

都是泊松方程的解，事实上。因此，更一般地，格林第三公式可写作

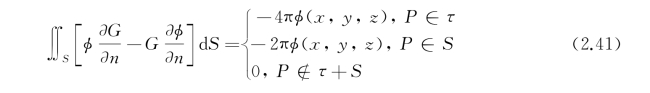
对二维问题也有类似的表达式。

当P∈S时，式（2.41）给出决定函数φ（P）≡φ（x，y，z）的积分方程：

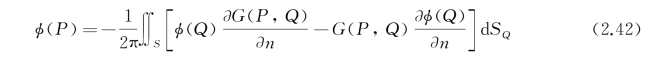
式中，P、Q都是边界面S上的点。若在S上给定

，即可得决定φ（P）的第二类弗雷德霍姆（Fredholm）积分方程；若在S上给定φ（Q），则可得到的第一类弗雷德霍姆积分方程。

G（P，Q）称为格林函数。在许多情况中，流场中除了物面边界外，还会出现各种形式的附加边界，如自由表面、池底、池壁等，上式中的积分表面应包括所有的问题中出现的边界面。然而，如果能选择一个合适的格林函数G（P，Q），使其不仅满足拉普拉斯方程（除P=Q点外），还满足附加的边界条件，那么一般来说，只要在感兴趣的物面边界上分布格林函数G（P，Q）及其法向导数就可以决定场内的速度势。G（P，Q）的选取应根据具体问题而确定，对此，在第5章中还将作些更具体的讨论。

由前面关于拉普拉斯方程解的唯一性讨论已知，如果在全部边界上给出φ值，则场内速度势就唯一地确定下来，显然，边界上的∂／∂n也是唯一确定的；反之，若给出边界上的∂／∂n值，场内（包括边界上）的速度势也必然是唯一的。因此，就有可能仅用点源形式的格林函数或仅用点偶形式的格林函数（即格林函数G（P，Q）的法向导数）在物面上的分布来表达流场中的势函数。