拉普拉斯方程解的唯一性在船舶波浪上的运动理论中的意义

由前面的讨论可知，在无旋条件下，制约均匀、不可压缩理想流体的基本方程就是拉普拉斯方程。然而实际问题是千变万化的，因而遵守同一拉普拉斯方程的流动也可以有种种不同的形式。这些实际问题的差别，在数学上有所谓的边界条件和初始条件来规定，它们通称为定解条件。相应地，在给定的定解条件下求解控制微分方程的数学问题称为定解问题。

对于确定性的现象来说，一个基本正确地（但总是近似地）描述所考察的物理模型的微分方程的定解问题，其解应该是存在的、唯一的并稳定的，即要满足解的存在性、唯一性和对定解条件的连续依赖性。这三者通称为定解问题的适定性。对适定性进行一定的考察，有助于我们初步判定所抽象的定解问题是否合理、附加的定解问题是否恰当，对求解能起一定的指导作用。关于适定性方面的严格论述，可参见相关的数理方程专著。本节中仅讨论拉普拉斯方程解的唯一性问题，考察在何种定解条件下，拉普拉斯方程的解才是唯一的。

在给定的均匀、不可压缩理想流体无旋流的流场中，流体总动能可表示为

式中，τ为所研究的领域。在本书讨论的范围内，我们可认为流域是单连通域，速度势是单值的。按关系式

和高斯（Gauss）公式，流体动能可写成

式中，S为流域的所有边界，n为流体边界上的单位外法线矢量。由此可见，边界上的速度势φ及其法向导数值决定了流场内流体的运动。

设在流场中存在两个势函数，分别记为φ1和φ2，它们均满足拉普拉斯方程。现构造一个新的速度势Φ=φ1-φ2，它必然也满足拉普拉斯方程，代表一种新的流动，其速度场为ΔΦ。按式（2.10），这个新流场的动能应该是(www.xing528.com)

显然，只有当EФ≡0时，才能说Ф代表的是静止流场，场中流体速度处处为零；也就是说φ1与φ2代表的是同一流动。这时，或者φ1=φ2，或者两者之间差一常数，但即使属于后一情况，由于常数对速度场没有影响，可以略去不计。因此，可以认为只有在EФ≡0时，场内速度势φ的解是唯一的。从式（2.11）可见，下列三种情况可使EФ≡0。

（1）在整个边界上给定φ1=φ2=φ，这种情况叫作第一类边值问题或狄利克雷（Dirichlet）问题。

（2）在整个边界上给定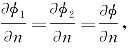这时叫作第二类边值问题或诺埃曼（Neumann）问题。

（3）在部分边界上给出φ1=φ2=φ，在余下部分边界上给出此谓混合边值问题（mixed boundary problem）。

需要指出的是，边界系指所有的流场边界。在无界流场中应包括无限远处的辐射条件。若遗漏某些边界，则不能保证解的唯一性。当全部边界上给定后，整个流场中的速度势就唯一确定下来，从而在边界上也是确定的，因此，φ和不能在边界的同一处上互相独立地给出。在同一部分的边界上，若已经给出值，就不能同时再给出别的条件，因为这时已经能够保证解的唯一性，此时担心的应该是存在性，即限制条件是否过多。

另外，应该注意边界条件是物理条件，它是由具体物理问题所规定的，而不是随意给出的。因此，并不意味着边界上只能给出而不能给出别的形式的条件。但是，在任何情况下，一旦能计算得出边界上的值，解就被唯一地规定了。事实上，之后有关章节中提到的线性化自由面条件即是有异于的一种边界条件形式，它状如，其中a、b、c均为已知常数，亦有专著将这种形式的边界条件叫作第三类边界条件。