SVM分类器在无人机与LiDAR观测中的应用

SVM是一种基于统计学习理论的机器学习算法，采用结构风险最小化原理，在最小化样本误差的同时缩小模型的泛化误差，以提高模型的泛化能力（Cortes和Vapnik，1995）。与传统机器学习算法采用经验风险最小化准则不同，SVM采用结构风险最小化准则：将函数集分为一个函数子集序列，使各个子集按照VC维的大小排列；在每个子集中寻找较小经验风险，在子集间考虑经验风险和置信范围，取得实际风险的最小。SVM的基本原理如下：

针对两类分类问题，yi∈{-1，+1}表示样本所属类别。SVM分类器通过非线性变换样本投影到某个高维的特征空间φ（x），通过寻找一个最优的超平面（Optimal Separating Hyperplane，OSH）来对两个类别进行区分，该超平面的判别函数公式为：

式中，w为权向量，b为偏移量。与OSH平行且在平面f（x）=±1上的训练样本称之为支持向量（Support Vectors，SVs），如图3.4所示。

SVM的分类过程是通过最大化两个超平面间的距离和最小化训练样本的分类误差确定OSH：

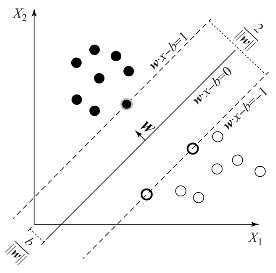
图3.4　SVM二维线性可分示意图

式中，εi是松弛变量用来考虑不可分的样本；C为惩罚系数，用来控制区分函数的形状，影响SVM的泛化能力。公式（3-13）的最小化问题可以通过Lagrange对偶优化来解决，同时，对公式（3-12）可以用核技巧在低维空间来表示高维特征φ（x）：(www.xing528.com)

式中，K（xi，xj）表示核函数，SVs表示支持向量的集合。常用的核函数有两种：

多项式函数（Polynomial Kernel，PK）：

其中，t为多项式函数的阶数。

径向基函数（Radial Basis Function，RBF）：

式中，γ为RBF函数的宽度。

当用SVM来解决多类分类问题时，一般有两种解决方法：一对一（One Against One，OAO）和一对多（One Against All，OAA）。其中，OAO是对任意两类问题使用同一个SVM分类器，采用投票的方式确定样本所属的类别；与OAO不同，OAA是针对L类分类问题选用i个分类器，利用第i个分类器来区分第i个类别与其他所有类别，通过对比SVM距离函数f（x）来确定样本所属类别。