以实验2为例评估SCN-SfM算法的重建模型精度。实验区内均匀布设了16个地面控制点（见图2.31），用于SCN-SfM重建点云的坐标转换与精度评估（注：图2.31中P2号控制点出现测量错误，本研究在精度评估中未考虑该点）。本研究利用差分GPS测量控制点坐标，保证每个控制点的测量误差小于2 cm。
图2.31 实验2影像及地面控制点分布
采用DN-SfM、MCN-SfM、TCN-SfM算法和SCN-SfM算法对实验2中数据进行处理，得到该研究区的三维点云（见图2.28）。为提高控制点选取精度，采用PMVS算法对上述方法重建的稀疏点云进行加密，得到相应的致密点云。图2.32为采用本研究方法得到的该研究区的致密点云，点云密度约为40点/m2，可准确选取实验区中15个地面控制点的点云坐标。其他3种方法生成的致密点云如图2.28、图2.29所示。本研究采用七参数坐标转换方法，将点云坐标系转换到WGS-84坐标系，然后计算转换后的地面控制点坐标与GPS-RTK测量坐标的残差，记为Δx，Δy，Δz。
图2.32 利用SCN-SfM和PMVS算法生成的实验2致密点云
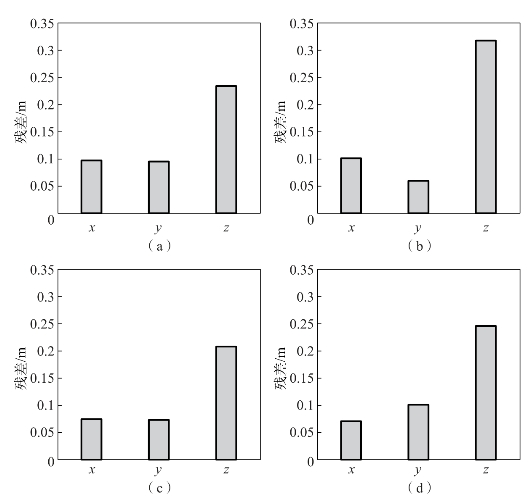
由于坐标转换过程未改变算法本身的重建过程，因此上述控制点坐标残差（Δx，Δy，Δz）主要为SfM重建算法的拉伸和局部畸变误差，可以作为评估上述4种方法重建模型相对优劣的标准。图2.33为不同SfM算法重建点云在x、y和z方向的平均残差。结果表明，4种SfM算法重建模型的精度基本一致，x和y方向的残差标准差约为10×GSD，z方向的残差标准差约为13×GSD（注：GSD表示影像地面分辨率，2.6 cm/像素）。
(www.xing528.com)
图2.33 不同SfM算法重建点云在xyz方向上的残差
图2.34为DN-SfM、MCN-SfM、TCN-SfM和SCN-SfM算法得在xy平面和z方向的平均残差。结果表明：部分地面控制点在z方向的残差方向相反且残差值较大，说明重建模型的残差主要来源于SfM算法重建过程中的局部畸变，而这种情况在MCN-SfM算法的重建结果中最为明显。究其原因，MCN-SfM算法中删除了部分影像，导致影像匹配稳定性差，造成相机自标定误差变大。由此可进一步推断：SfM算法中的局部畸变主要源于相机的自标定误差。
图2.34 不同SfM算法重建控制点在xy平面和z方向的残差（右下虚线表示10 cm）
（a）DN-SfM；（b）MCN-SfM；（c）TCN-SfM；（d）MCN-SfM
图2.35为不同SfM算法重建模型的测距相对误差，结果基本一致，精度小于±0.005%，表明SCN-SfM算法在显著提升重建效率的同时未损失重建模型的精度。
图2.35 不同SfM算法重建点云的测距相对误差
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
