本节的目的是验证HDB-MST提取影像拓扑骨架SCN的稳定性,期望SCN中保留的邻接边少、权重大、结构性强。理论上,上述期望要素之间相互制约,尚不能对其定量表达。因此,本研究通过定性分析SCN中保留邻接影像的分布情况和重叠度来测试骨架提取的稳定性。为便于描述,本书仅以直接分析法(下同)构建影像TCN为例测试相应SCN的稳定性。
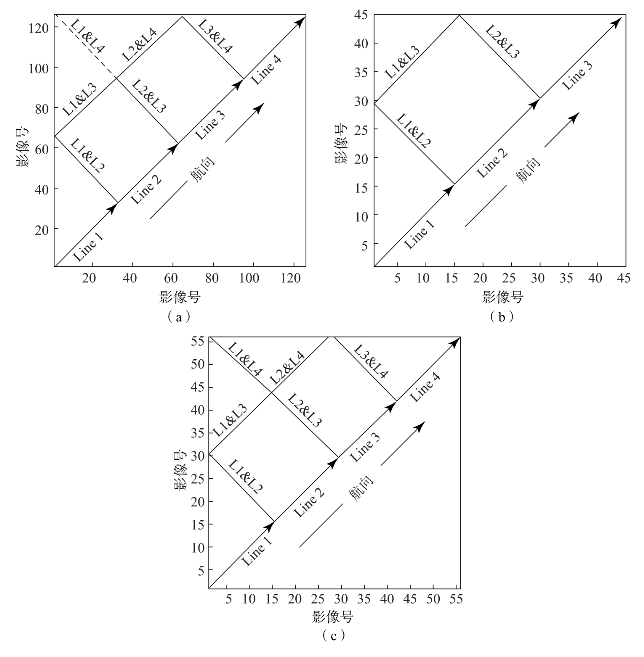
图2.19 航线示意图
(a)实验1;(b)实验2:(c)实验3
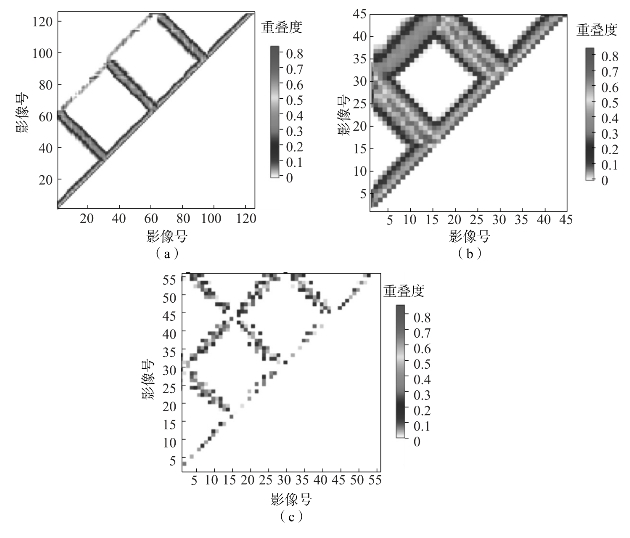
图2.19为3组实验中低空测量的航线示意图。图2.19中,对角线代表航向影像间的拓扑关系,对角线以外的线代表任意两条航带旁向影像间的拓扑关系。图2.20表示各实验中影像TCN的邻接矩阵,由n×n的栅格组成(n为影像数),每个栅格代表对应序号邻接影像的重叠度。为对比分析,本研究将3组实验中邻接矩阵的影像重叠度归一化相同范围(0~0.85),并按颜色深度表示。图2.20(a)(b)分别为实验数据1和2的影像邻接矩阵,因其数据采集过程中,受风速影响较小,飞行航线规则,影像采集规律,序列影像对间的重叠度变化不大。其中,图2.20(a)中航线方向上相邻影像间的重叠度集中在0.7~0.85,范围大于旁向方向相邻影像的重叠度(0.3~0.45);非邻近影像间的重叠度较小(0.25),尤其是间隔航带间邻接影像的重叠度,为0.02~0.08。图2.20(b)所示邻接矩阵在空间分布形态上与图2.20(a)类似,但其旁向方向相邻影像的重叠度较大,为0.65~0.7。图2.20(c)为实验3影像的拓扑邻接矩阵。与实验1和2不同,该实验在数据采集过程中无人机受风速、相机曝光延时等条件影响,导致无人机飞行航线不规则,图2.20(c)中,仅有少数邻接影像的重叠度较大,为0.7,其他邻接影像的重叠度均较小,集中在0.1~0.5范围。
 (https://www.xing528.com)
(https://www.xing528.com)
图2.20 影像拓扑TCN的邻接矩阵
(a)实验1;(b)实验2;(c)实验3
图2.21为采用HDB-MST算法生成的3组实验影像的SCN,图2.21中表示邻接影像的数据较TCN明显减少。图2.21(a)(b)分别为实验1和实验2的SCN。图2.21(a)和图2.21(b)中可见,两组实验影像的SCN中保留了航向上几乎所有的和旁向上少量的邻接关系。此外,两图中没有保留任何非邻近航带影像间的邻接关系,说明大量重叠度过小的邻接关系已被删除。图2.21(c)为实验3影像的SCN,与图2.21(a)(b)不同,该图中仅保留了航向上少量的影像邻接关系,而且保留了旁向上大部分的影像邻接关系。即便如此,图2.21(c)中仍保留了重叠度较大的影像邻接关系而删除了重叠度较小的部分影像邻接关系。由此发现:基于HDB-MST算法提取SCN的结果主要与影像间的重叠度大小有关,而与影像在航线中的位置关系较小。此外,本研究提取的影像SCN除了保留了航线方向上的主要邻接关系外,还保留了部分旁向影像邻接关系,保证了原影像TCN的“骨架”结构特征。综上所述,本研究提取的影像SCN达到了研究预期,同时兼顾了SCN中对边的数目、权重和拓扑结构的合理约束。
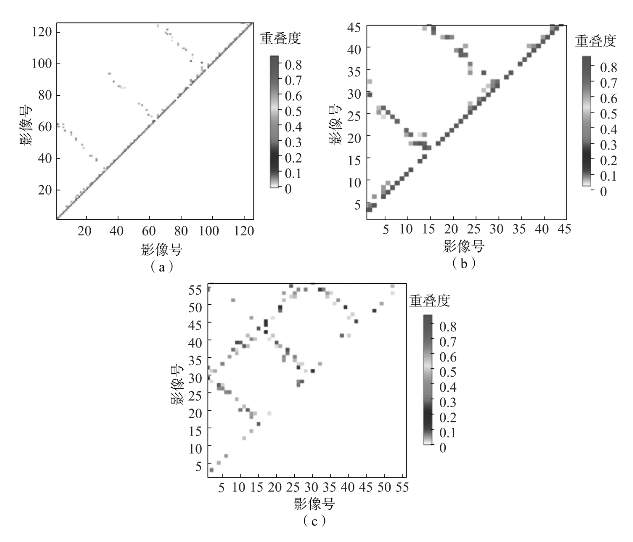
图2.21 影像拓扑骨架SCN的邻接矩阵
(a)实验1;(b)实验2;(c)实验3
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




