
图1.3 运动恢复结构算法流程图
运动恢复结构(SfM)算法属于计算机视觉的研究范畴,是本书研究低空影像三维重建的基础。该算法通过在多幅重叠影像中检测匹配特征点集,采用数值方法恢复出相机参数(位置、姿态)与场景三维信息。早期研究者参照视差原理利用两幅影像的少量匹配点对恢复出对应点的三维信息(Longuet-Higgins,1987;Ullman,1979)。随着对影像视觉重建需求的增加,众多学者对SfM算法做了大量研究,使得SfM算法逐渐完善(D'Apuzzo,2003;Pollefeys等,2000;Tomasi和Kanade,1992)。该算法主要包括4个步骤:输入图像、特征提取、特征匹配和恢复重建(见图1.3)。其中,特征提取是在影像中检测需匹配的特征点集,常用的算法有SIFT算法(Lowe,1999,2004)、SURF算法(Bay等,2006)和其改进算法(Ke和Sukthankar,2004)等。特征匹配是SfM算法的核心部分,用来确定不同影像之间的同名匹配点,继而建立影像之间的几何约束关系。恢复重建是采用三角化技术对匹配的特征点集进行优化,通过最小化同名匹配点的重投影误差,计算出相机参数和同名匹配点的三维点坐标。由于SfM算法在重建过程中可实现相机自标定,对影像要求低,且不依赖于特定假设条件,通用性好,已被广泛应用于文物保护(El-Hakim等,2004)、城区规划(Carozza等,2014)、虚拟现实(Feng等,2014)及灾害应急管理(Bulatov等,2014;Wilson等,2018)等领域。
然而,SfM算法的重建耗时随着处理影像数目的增多呈二次幂指数增长,导致处理大数据影像集时效率低。分析表明,引起耗时增多的因素主要有两方面:
(1)冗余匹配:目标影像中的特征点遍历搜索全局待匹配影像产生大量冗余匹配;
(2)迭代平差:新增匹配影像与已重建影像的迭代平差。(https://www.xing528.com)
目前,国内外学者对后者的研究较多,例如,Snavely等(2008)采用图论方法简化了特征匹配后的影像连接关系,约束影像迭代平差的数量,实现了“一日罗马”快速三维重建。Toldo等(2015)根据特征匹配后的影像邻接关系及特征点分布情况对影像集进行分块,减少了单次重建过程中的影像数目;然后基于每块数据集中影像特征点的连接关系进行影像迭代平差和恢复重建。该方法通过减少大数据量影像的迭代平差耗时,达到提高SfM重建效率的目的。大量实验表明,在SfM算法的整个环节中,影像遍历匹配的耗时最为显著。因此,针对大数据量影像重建,提高其重建效率的最有效方法是解决影像间遍历匹配的问题。针对该问题,国内外学者已有一些研究。其中,一种有效的手段是在特征匹配之前对影像集的拓扑关系进行预判,构建影像邻接矩阵(Topologically Connected Network,TCN),以此作为影像匹配的索引,约束特征匹配的搜索范围,避免冗余匹配。针对该类问题,常用的方法有:
(1)间接索引法,如词汇树法(Chum等,2007)和降采样特征匹配法。
(2)直接分析法,如相对定向法(Rupnik等,2015)和GPS定位法(Douterloigne等,2010)等。
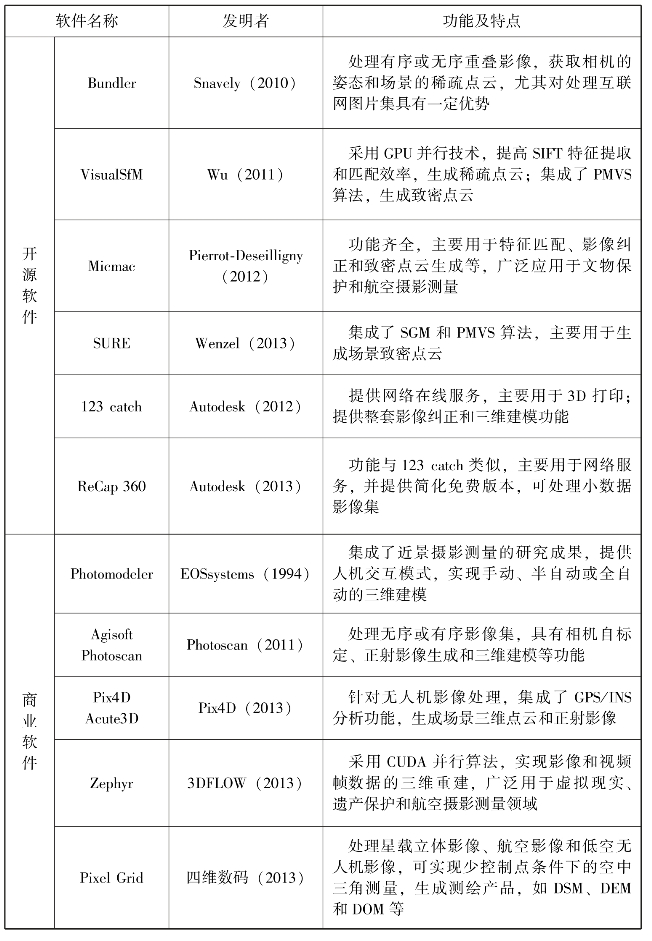
此外,Wu(2011)采用GPU并行技术提出了VisualSfM算法,提高了三维重建效率;Furukawa(2007)提出了多目视觉的致密点云重建算法(Dense Multi-View 3D Reconstruction,DMVR),在SfM算法重建稀疏点云的基础上提高了点云密度。近些年来,相关的开源软件和商业软件相继出现(见表1.1),使得人们利用数码相机获取地物的三维信息变得越来越容易。然而,当前针对低空无人机影像的三维重建软件尚少,即使Micmac、Pix4D、Photoscan和Pixel Grid软件具有处理低空影像的能力,但与三维重建效率方面的要求尚有较大的距离,这在大区域灾场三维重建中尤为重要。
表1.1 运动恢复结构软件系统归纳
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




