1.多项式(Polynomial)的表达与创建
(1)多项式的表达.
MATLAB用行矢量表达多项式系数(Coefficient),各元素按变量的降幂顺序排列.如多项式为:
P(x)=a0xn+a1xn-1+a2xn-2+…+an-1x+an,
则其系数矢量(Vector of coefficient)为:
P=[a0 a1…an-1 an]
如将根矢量(Vector of root)表示为:
ar=[ar1 ar2…arn]
则根矢量与系数矢量之间关系为:
(x-ar1)(x-ar2)…(x-arn)=a0xn+a1xn-1+a2xn-2+…+an-1x+an.
(2)多项式的创建.
①系数矢量的直接输入法.
利用poly2sym函数直接输入多项式的系数矢量,就可方便地建立符号形式的多项式.
例1 创建多项式x3-4x2+3x+2.
poly2sym([1-4 3 2])
结果为:
ans=x^3-4*x^2+3*x+2
②由根矢量创建多项式.
通过调用函数p=poly(ar)产生多项式的系数矢量,再利用poly2sym函数就可方便地建立符号形式的多项式.
注:①根矢量元素为n,则多项式系数矢量元素为n+1;
②函数poly2sym(pa)把多项式系数矢量表达成符号形式的多项式,缺省情况下自变量符号为x,可以指定自变量;
③使用简单绘图函数ezplot可以直接绘制符号形式多项式的曲线.
例2 由根矢量创建多项式.将多项式(t-6)(t-3)(t-8)表示为系数形式,再转化为符号形式并作图.

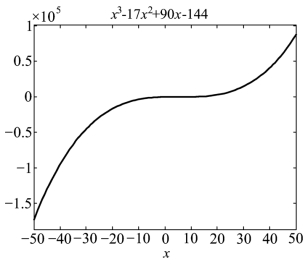
图2.4.1 (t-6)(t-3)(t-8)的图形
结果为:
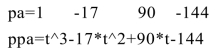
注:含复数根的根矢量所创建的多项式要注意:
①要形成实系数多项式,根矢量中的复数根必须共轭成对;
②含复数根的根矢量所创建的多项式系数矢量中,可能带有很小的虚部,此时可采用取实部的命令(real)把虚部滤掉.(https://www.xing528.com)
例3 由给定复数根矢量求多项式系数矢量及符号表达式.

结果为:
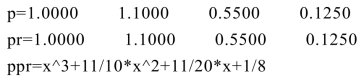
进行多项式的求根运算时,可直接调用求根函数roots,poly和roots互为逆函数.
例4 求x3-6x2-72x-27的根.
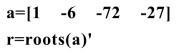
结果为:
![]()
MATLAB约定,多项式系数矢量用行矢量表示,根矢量用列矢量表示.
2.多项式的乘除运算
多项式乘法用函数conv(a,b)实现,除法用函数deconv(a,b)实现.
例5 a(s)=s2+2s+3,b(s)=4s2+5s+6,计算a(s)与b(s)的乘积.
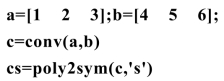
结果为:
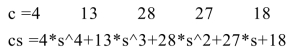
例6 展开(s2+2s+2)(s+4)(s+1).(多个多项式相乘)
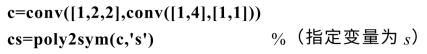
结果为:
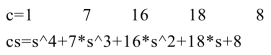
例7 求多项式s4+7s3+16s2+18s+8分别被(s+4),(s+3)除后的结果.

结果为:

3.其他常用的多项式运算命令
![]()
例8 a(s)=s2+2s+3,计算a(1).
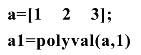
结果为:
a1=6
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




