1.算术运算(Arithmetic Computation)
MATLAB提供了两种运算方式:
(1)数组运算方式(Array computation):在数组中对应元素之间进行运算;
(2)矩阵运算方式(matrix computations):将标量当作1×1阶矩阵,一维数组当作一行或一列的矢量(即1×n阶或n×1阶的矩阵),二维数组当作m×n阶矩阵,然后按照矩阵的运算规则进行运算(这部分内容本书仅介绍加减乘).
注:两者输入的形式和书写方法相同,差别仅在于用不同的运算符号,执行不同的计算过程,数组的运算是对应元素之间的运算,而矩阵运算是根据矩阵的运算规则进行的.
(1)加、减运算(addition and subtraction).
矩阵与数组的加减运算没有区别,运算符均为“+”、“-”,运算方法相同,但两个运算对象必须是同阶矩阵,否则将给出错误信息.如下例:

运行结果给出错误信息:
![]()
Matrix dimensions must agree.(矩阵的维度必须一致)
但标量,即1×1阶矩阵可以和其他不同维数的矩阵进行加减运算,如:a+5

(2)乘除运算(Multiplication and division).
矩阵在进行乘除运算时与通常的运算符号相同(*,/,\),而数组在进行乘除运算时要在通常的符号前加“.”,如:“.*”和“./”(或“.\”)
①矩阵乘法:矩阵相乘的条件是前一矩阵的列数与后一矩阵的行数相同,如输入
x=[1 2 1;2 1 3];y=[2 0;1 3;0 1];
则结果为:

②数组的乘法(Array multiplication)
条件:a,b两数组必须有相同的维数.a.*b表示a和b中对应元素之间相乘,即c(i,j)=a(i,j)*b(i,j).如:
![]()
![]()
结果为:
![]()
③矩阵除法(略).
④数组的除法(Array division).
条件:a与b必须具有相同的维数.符号:“.\”或“./”,运算结果相同,a.\b表示b中的元素分别除以a中的对应元素,即c(i,j)=a(i,j)\b(i,j)=b(i,j)/a(i,j).如:
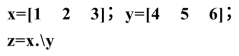
结果为:
![]()
(3)乘方(Power).
①矩阵的乘方(略).
②数组的乘方(Array power).符号:“.^”
条件:在底与指数均为数组的情况下,要求它们的维数必须相同.
a.当底和指数为同样大小的数组时,x.^y为对应的元素作乘方运算.如:
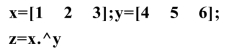
结果为:
![]()
这时执行的实际运算为:
![]()
b.若指数是标量p,执行的运算是底的每一个元素执相同幂次的运算.即
![]()
如:

得到结果为:
![]()
这时执行的运算为:
![]()
c.若底是一个标量p,指数是一个数组,执行的运算是用指数数组的每个元素对底进行乘方运算,即z(i,j)=p^x(i,j),形成新的数组.如:
![]()
结果为:
![]()
这时执行的运算为:
![]()
(4)转置(Transpose):行列转置,符号:“'”(用enter键左侧的按键输入)
如计算矩阵a的转置:
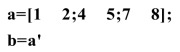
结果为:

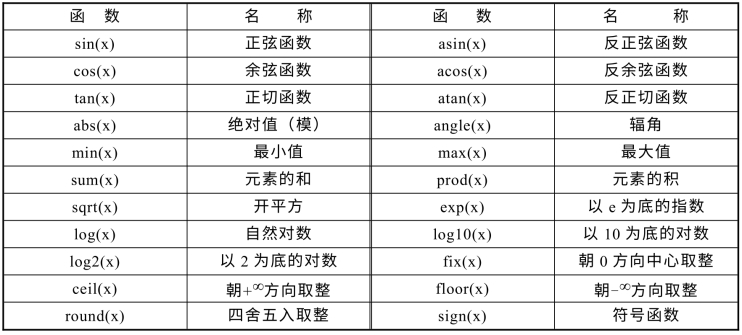
2.数学函数 (Mathematic function)(见表2.3.1)
基本函数(Elementary function):三角函数(Trigonometric Function)、指数函数(Exponent function)、复数函数(Complex function)、取整和求余函数(round and remain function)等.
表2.3.1 常用基本数学函数
例1 朝零方向取整.

结果为:
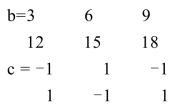
三角函数按弧度计算.有两个函数需要特别加以区分,就是除后取模mod(x,y)与y符号相同,除后取余数rem(x,y)与x符号相同,当x与y符号相同时,mod(x,y)等于rem(x,y).
例2 求余函数rem.

结果为:
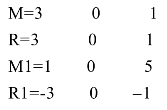
3.关系运算与逻辑运算(Relational calculus and Logical operation)
(1)关系运算(Relational calculus).
条件:对于两个矩阵的关系运算,两边的矩阵必须具有同样尺寸.
关系运算符(Relational operator):
<小于(less than)、<=小于等于(less than or equal to)、>大于(greater than)、>=大于等于(greater than or equal to)、==等于(equal to)、~=不等于(not equal to,NE).
例3 标量关系运算和矩阵关系运算.

结果为:

在程序的流程控制中,关系运算符常配合if,while,for,switch等控制命令使用.
(2)逻辑运算(Logical operation).
逻辑运算符(Logical operator):
&与(AND),|或(OR),~非(NOT)(https://www.xing528.com)
条件:对于两个矩阵的逻辑运算,两边的矩阵必须具有同样尺寸.
“~”是一元算符,当a为零时,返回信息为1,为非零时,返回信息为0.
例4 逻辑运算:

结果为:

4.基本字符处理功能(Elementary symbolic treatment function)
(1)字符数组的建立(Setting of symbolic array):
①字符串(string of character)就是字符数组(Character arry),MATLAB中所有字符串都用单引号界定后输入或赋值.例如:

结果为:

字符串中空格也是字符,上例为1×11阶矩阵.
②如同数值型矩阵一样,可以用方括号(square bracket)将字符串合并成更大的串.例如:
s=[s1,'!']
得结果:
s=Hello Kitty!
③可以从一个字符串中提取子串(sub string).例如:
ss=s(7:11)
得结果:
ss=Kitty
(2)字符数组的运算(Operation of symbolic array).
①字符以ASCⅡ码存储,用double命令可以查出字符的ASCⅡ码值.如:运行double(s1)得s1码值为:
![]()
②用char命令可以实现ASCⅡ码向字符的转换.如:执行char[65 66 67 68]得:
ans=ABCD
③trcmp函数具有比较字符串的功能.如执行strcmp(str1,str2),返回1表示str1=str2,返回0表示str1≠str2.
5.建立特殊数组(矩阵)
(1)用标准函数建立数组(或矩阵):用于辅助编程或运算的一些基本数组或矩阵.

(2)由小数组建立大数组:大数组可由方括号中的小数组建立,如有矩阵
![]()
可利用它建立一个大矩阵:
![]()
得到:

注:同一行的各个小数组要有相同的行数,在同一列上的各个小数组要有相同的列数.
(3)冒号“:”的使用:
产生一维数组(Initialize a one dimensional array).如:
x=1:5
得到:
![]()
即产生一个1到5的单位增量的一维数组.当然,也可产生任意增量的一维数组,如:
y=0:pi/4:pi
得到:
![]()
z=6:-1:1
得到:
![]()
(4)下标的使用(The using of subscript):
①元素定位:单个的数组元素的位置可在括号中用下标来表达.如:

其中a(3,3)=9,a(1,3)=3,a(3,1)=7,可用带下标的元素表达式进行运算和赋值产生新元素.如执行a(3,3)=a(1,3)+a(3,1)),则有:

下标可以是一个一维数组.对于矩阵来说,利用下标可以调用某些元素构成新的子数组.设b是一个10×10阶数组,则b(1:5,3)指b中的第1行到第5行处于第三列的元素组成5×1阶子数组.
b(1:5,7:10)指前5行处于后四列中的元素构成5×4阶的子数组.
b(:,[3,5,10])=c(:,1:3)表示将数组c的前三列赋值给数组b的第3、5、10列.
a(:,n:-1:1)即为由原来a数组中取n至1负增长的列元素组成一个新的数组,即将a矩阵左右翻转.
例5 矩阵元素的定位.

得到:

②改变数组尺寸.
例6 将一个2×3阶的数组改变为6×1阶.

得到:
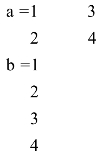
即将a矩阵按列拼接为加长列向量.也可利用(:)置换数组元素.如:
a(:)=11:14
得到:

改变数组尺寸可以reshape命令实现.如:

得到:

也可以将矢量变为矩阵.例如
a=reshape(1:10,2,5)
得到:

③空数组:语句[]将一个0×0阶的数组,存在于工作空间,具有空尺寸,与起清除工作空间的clear命令完全不同.
如n<1时,程序x=1:n会产生空数组x.
若要将某些行与列从数组中移去,采用将其置为空数组是一种有效的方法.如
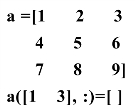
得到:
![]()
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




