1.解非线性方程组、不等式组
LINGO可以求解方程组和不等式组,但每次运行只能求得1解,不能求得全部解.
例1 求解非线性方程组:
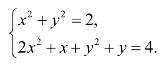
求解LINGO代码如下:
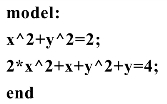
计算的部分结果为

2.装配线平衡模型
一条装配线含有一系列的工作站,在最终产品的加工过程中每个工作站执行一种或几种特定的任务.装配线周期是指所有工作站完成分配给它们各自的任务所花费时间中的最大值.平衡装配线的目标是为每个工作站分配加工任务,尽可能地使每个工作站执行相同数量的任务,其最终标准是装配线周期最短.不适当的平衡装配线将会产生瓶颈——有较少任务的工作站将被迫等待其前面分配了较多任务的工作站[23].
这个模型的目标是最小化装配线周期.有两类约束:
(1)要保证每件任务只能也必须分配至一个工作站来加工;
(2)要保证满足任务间的所有优先关系.
例2 有11件任务(A~K)分配到4个工作站(1~4),任务的优先次序如图1.5.1所示.每件任务所花费的时间见表1.5.1.
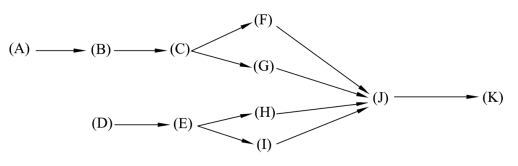
图1.5.1 任务的优先次序
表1.5.1 每项任务所花费的时间

解 设 it——任务i所需时间,建立模型如下:
it——任务i所需时间,建立模型如下:
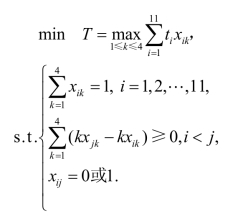
非线性规划(目标函数非线性)转化为线性规划增加约束:(https://www.xing528.com)
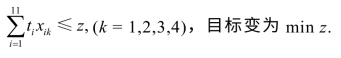
LINGO代码如下:

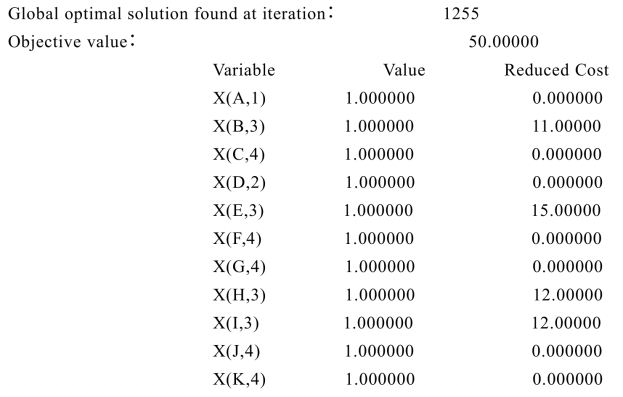
计算的部分结果(仅列出取值为1的决策变量)为
3.排列排序问题
例3 有4名同学到一家公司参加3个阶段的面试:公司要求每个同学都必须首先找公司秘书初试,然后到部门主管处复试,最后到经理处参加面试,并且不允许插队(即在任何一个阶段4名同学的顺序是一样的).由于4名同学的专业背景不同,所以每人在3个阶段的面试时间也不同,如表1.5.2所示(单位:分钟):
表1.5.2 面试时间

这4名同学约定他们全部面试完以后一起离开公司.假定现在时间是早晨8:00,问他们最早何时能离开公司[24]?
解 记tij为i同学完成j阶段面试所需时间,xij为i同学开始j阶段面试所处的时间,则
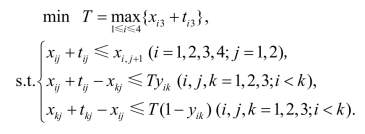
可将目标函数线性化改写为
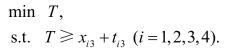
求解程序如下:


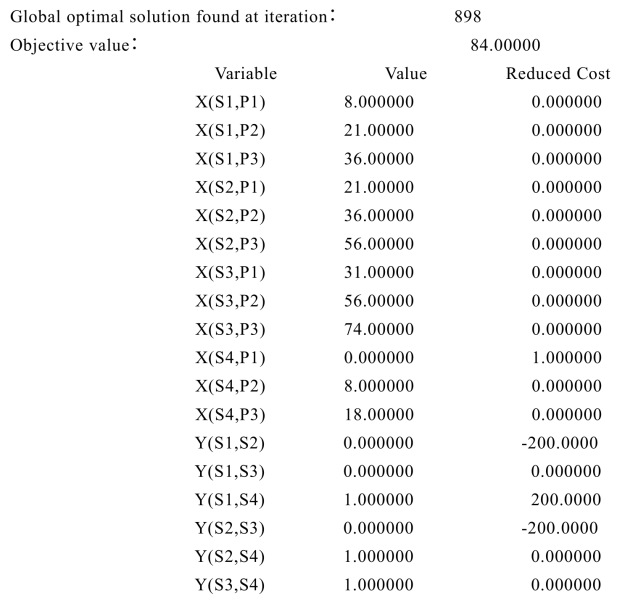
计算的部分结果为:
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




