一、多项式最小二乘拟合
在MATLAB的最小二乘拟合中,用得较多的是多项式拟合,其命令为:
a=polyfit(x,y,m)
其中x=(x1,x2,…,xn),y=(y1,y2,…,yn),a=(a1,a2,…,am+1).
计算多项式在x处的值y可用以下命令:
y=polyval(a,x)
例1 对表10.4.1中实验数据作二次多项式拟合.
表10.4.1 实验数据

即要求出二次多项式f(x)=a1x2+a2x+a3中的a=(a1,a2,a3),使得![]() 最小.
最小.
方法1 用多项式拟合的命令.
输入以下命令:

计算结果为:
![]()
图形如图10.4.1所示.

图10.4.1 多项式拟合结果
方法2 用图形窗口菜单Tools|Basic Fitting.
首先作散点图,输入以下命令:

在图形窗口菜单点击Tools|Basic Fitting,弹出窗口图10.4.2.在拟合图形类型(Plot fits)窗口中勾选相应的拟合函数类型(这里选择抛物线quadratic),勾选显示方程(Show equations),绘制残差图(Plot residuals),显示残差的模(Show norm of residuals).得到图形拟合结果,如图10.4.3所示.

图10.4.2 基本拟合对话框(https://www.xing528.com)

图10.4.3 图形拟合结果
二、非线性最小二乘拟合
在最小二乘拟合中,若要寻求的函数f(x)是任意的非线性函数,则称为非线性最小二乘拟合.MATLAB的优化工具箱中提供了求非线性最小二乘拟合的函数:lsqcurvefit.使用时,要先建立M-函数文件fun.m.
设已知xdata=(x1,x2,…,xn),ydata=(y1,y2,…,yn),lsqcurvefit用以求含参量x(向量)的向量值函数
F(x,xdata)=(F(x,x1),…,F(x,xn))T
中的参变量x(向量),使得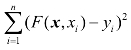 最小.
最小.
基本输入格式为:
![]()
其中x0为迭代的初值,r为残差模.
例2 用表10.4.2中实测数据拟合函数c(t)=a-be-kt中的参数a,b,k.
表10.4.2 实测数据

解 该问题即解最优化问题:
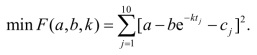
用命令lsqcurvefit,此时
![]()
(1)编写M文件curvefun.m.

(3)运行主程序,得结果:
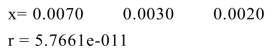
即拟合得到的模型为c(t)=0.007-0.003e-0.002t,拟合效果如图10.4.4所示.

图10.4.4 例2拟合结果
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




