最小二乘法：实现最佳曲线拟合

曲线拟合问题是指：已知平面上n个点(xi，yi)，i=1，2，…，n，xi互不相同，寻求函数f(x)，使f(x)在某种准则下与所有数据点最为接近，即曲线拟合得最好.

1.最小二乘拟合

最小二乘法是解决曲线拟合最常用的方法，其基本思路是，令

其中rk(x)是事先选定的一组函数，ak是待定系数(k=1，2，…，m，m＜n).寻求a1，a2，…，am使

最小，称为最小二乘准则.这种拟合方法称为最小二乘拟合.

（1）系数ak的确定.

为求a1，a2，…，am使J达到最小，只需利用极值的必要条件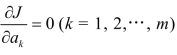，得到关于a1，a2，…，am的线性方程组：

最小二乘拟合可由解超定方程：

求得，其中

当{r1(x)，…，rm(x)}线性无关时，RTR可逆，方程组（10.3.3）有唯一解.在MATLAB中，此解为：A=R\y.

（2）r1(x)，r2(x)，…，rm(x)的选取.

面对一组数据(xi，yi)，i=1，2，…，n，用最小二乘法作曲线拟合时，关键是恰当地选取r1(x)，r2(x)，…，rm(x）.如能通过机理分析，知道y与x之间应该有什么样的函数关系，则r1(x)，r2(x)，…，rm(x)就容易确定；若无法知道y与x之间的关系，通常用数据作图，以直观地判断应该用什么样的曲线去拟合，常用的曲线有直线、多项式、双曲线、指数曲线等.实际操作中可以在直观判断的基础上，选几种曲线分别作拟合，然后比较，看哪条曲线的最小二乘指标J最小.

2.多项式拟合

特别地，若令(www.xing528.com)

则最小二乘拟合称为多项式拟合.

假设有已知数据(xi，yi)(i=0，1，2，…，n)，现求作一个不超过m(n＞m)次的多项式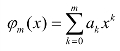，使得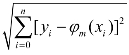取最小，亦即

取最小.

不难看出，以上多项式最小二乘拟合问题就是求解关于ak(k=0，1，2，…，m)的超定方程组：

的最小二乘解问题.根据方程组（10.3.3），它所对应的正规方程组为：

记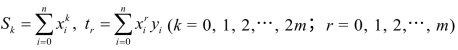，上述方程组可改为：

通过解正规方程组（10.3.7）便可解出ak，从而确定出拟合多项式φm(x).

多项式拟合的一般方法可归纳为：

（1）根据具体问题，确定拟合多项式的次数m；

（2）由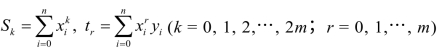，计算出Sk与tr；

（3）写出正规方程组（10.3.7）；

（4）解正规方程组，求出ak(k=0，1，2，…，m)；

（5）写出拟合多项式.