MATLAB一维插值问题解析

MATLAB在一维插值函数interp1中，提供了四种可供选择的插值方法，即线性插值、三次样条插值、三次插值和最近邻点插值（linear、spline、cubic、nearest）.其中interp1的格式为：

interp1(x，y，cx，'method')

其中x，y分别表示数据点的横、纵坐标向量，x必须单调；cx为需要插值的横坐标数据，cx不能超出x的范围；method为可选参数.对应于上述四种方法，可从以下四个值中任选一个：

①'nearest'——最近邻点插值；

②'linear'——线性插值（缺省值）；

③spline'——三次样条插值；

④'cubic'——三次插值.

例1　在12 h内，每隔1 h测量一次温度，温度依次为：

5，8，9，15，25，29，31，30，22，25，27，24.

试估计在3.2 h，6.5 h，7.1 h，11.7 h时的温度值.

解　输入命令：(www.xing528.com)

计算结果：

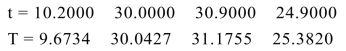
比较发现，样条插值与线性插值的结果不同.因为插值是一个估计或猜测的过程，应用不同的估计规则将导致不同的结果.

一个最常用的样条插值是对数据进行平滑，即给定一组数据，使用样条插值可以在更细的间隔内求值.

例2　在例1的条件下，每隔估计一次温度值.

解　由于数据点太多，最好用图形表示.输入命令：

图形如图10.2.1所示.

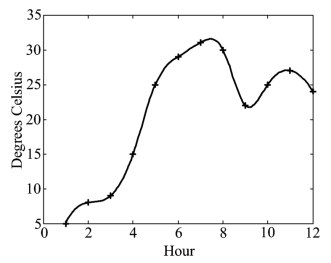
图10.2.1　样条插值