酶促反应速度与底物浓度关系数学模型

酶是一种具有特异性的高效生物催化剂，酶催化的反应称为酶促反应，它比相应的非催化反应快103～1017倍.某生化系学生为了研究嘌呤霉素在某项酶促反应中对反应速度与底物浓度之间关系的影响，设计了两个实验：一个实验中所使用的酶是经过嘌呤霉素处理的，而另一个实验所用的酶是未经嘌呤霉素处理过的，所得的实验数据如表9.2.1所示.试根据问题的背景和这些数据建立一个合适的数学模型，以反映这项酶促反应的速度与底物浓度以及嘌呤霉素处理与否之间的关系[20].

表9.2.1　嘌呤霉素实验中的反应速度与底物浓度数据（1 ppm=0.001‰）

【分析与假设】

记酶促反应的速度为y，底物浓度为x，两者之间的关系记作y=f(x，β)，其中β为参数.由酶促反应的基本性质可知，当底物浓度较小时，反应速度大致与浓度成正比（即一级反应）；而当底物浓度很大，渐进饱和时，反应速度将趋于一个固定值——最终反应速度（即零级反应）.下面的简单模型具有这种性质：

Michaelis-Menten模型：

在MATLAB中运行如下程序段1：

得到经过嘌呤霉素处理和未经处理的反应速度y与底物浓度x的散点图（见图9.2.1和图9.2.2）.从图形可以知道，模型（9.2.1）与实际数据得到的散点图是大致符合的.

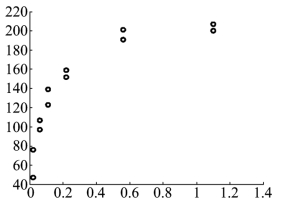
图9.2.1　y对x（经处理）的散点图

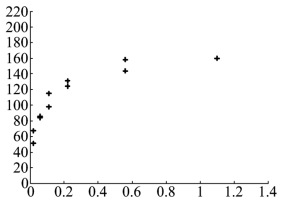
图9.2.2　y对x（未经处理）的散点图

首先对经过嘌呤霉素处理的实验数据进行分析（未经处理的数据可同样分析），在此基础上，再讨论是否有更一般的模型来统一刻画处理前后的数据，进而揭示其中的联系.

【线性化模型】

模型（9.2.1）关于参数β=(β1，β2)是非线性的，但是可以通过下面的变量代换化为线性模型：

模型（9.2.2）中的因变量对新的参数θ=(θ1，θ2)是线性的.

在上述程序段1的基础上添加如下程序段2：

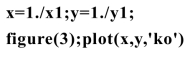
对经过嘌呤霉素处理的实验数据，作出反应速度的倒数与底物浓度的倒数的散点图

（见图9.2.3），发现在较小时有很好的线性趋势，而较大时出现很大的起落.

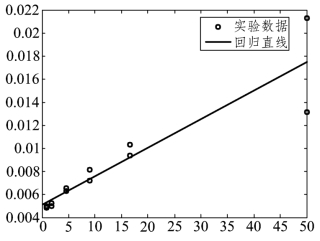
图9.2.3　的散点图和回归直线

在上述程序段1-2的基础上添加如下程序段3：

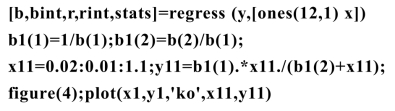
运行得到线性化模型（9.2.2）的参数θ1，θ2的估计和其他统计结果（见表9.2.2），以及根据

（9.2.2）式中β与θ的关系得到的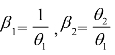的估计值（分别为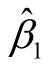=195.8020和=0.04840），还有原模型（9.2.1）与原始数据比较的拟合图（见图9.2.4）.

表9.2.2　线性化模型（9.2.2）参数的估计结果

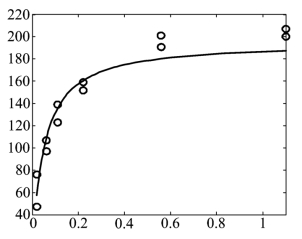
图9.2.4　用线性化得到的原始数据拟合图

由图9.2.4可以发现，在x较大时y的预测值要比实际数据小，这是因为在对线性化模型作参数估计时，底物浓度x较低（很大）的数据在很大程度上控制了回归参数的确定，从而使得对底物浓度x较高数据的拟合，出现较大的偏差.

为了解决线性化模型中拟合欠佳的问题，我们直接考虑非线性模型（9.2.1）.

【非线性模型及求解】

可以用非线性回归的方法直接估计模型（9.2.1）中参数β1和β2.模型的求解可利用MATLAB统计工具箱中的命令进行，格式为：

其中输入x为自变量数据矩阵，每列一个变量；y为因变量数据向量；model为模型的M函数文件名，M函数形式为y=f(beta，x)；beta为待估计参数，beta0为给定的参数初值.输出beta为参数的估计值，r为残差，J为用于估计预测误差的Jacobi矩阵.参数beta的置信区间用命令nlparci(beta，r，J)得到.

我们用线性化模型（9.2.2）得到的β作为非线性模型参数估计的初始迭代值，在上述程序段1-3的基础上添加程序段4及自定义函数“huaxue”（注意要单独一个文件保存）：

自定义M-函数“huaxue”:

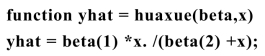
运行得到的数值结果如表9.2.3所示.

表9.2.3　模型（9.2.1）参数的估计结果(www.xing528.com)

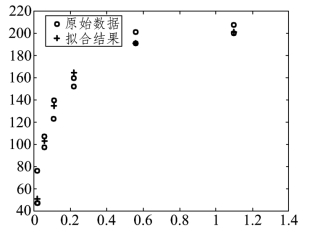
图9.2.5　模型（9.2.1）的预测图

拟合的结果直接画在原始数据图上（见图9.2.5）.程序中的nlintool用于给出一个交互式画面（见图9.2.6），拖动画面中的十字线可以改变自变量x的取值，直接得到因变量y的预测值和预测区间，同时通过左下方Export下拉式菜单，可输出模型的统计结果，如剩余标准差等，本例中剩余标准差s=10.9337.

从上面的结果可以知道，对经过嘌呤霉素处理的实验数据，在用Michaelis-Menten模型（9.2.1）进行回归分析时，最终反应速度为212.6837=.还容易得到，反应的“半速度点”（达到最终反应速度一半时的底物浓度x值）恰为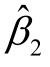0.0641=.以上结果对这样一个经过设计的实验（每个底物浓度做两次实验）已经很好地达到了要求.

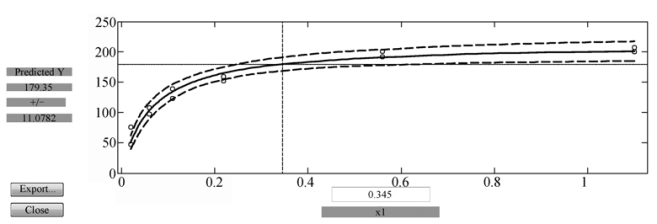
图9.2.6　模型（9.2.1）的预测及结果输出

【混合反应模型】

酶促反应的速度依赖于底物浓度，并且可以假定，嘌呤霉素的处理会影响最终反应速度参数β1，而基本不影响半速度参数β2.表9.2.1的数据（图9.2.1、图9.2.2更为明显）也印证了这种看法.模型（9.2.1）的形式可以分别描述经过嘌呤霉素处理和未经处理的反应速度与底物浓度的关系（两个模型的参数β会不同）.为了在同一个模型中考虑嘌呤霉素处理的影响，我们采用对未经嘌呤霉素处理的模型附加增量的方法，考察混合反应模型

其中自变量x1为底物浓度（即模型（9.2.2）中的x）；x2为一示性变量（0-1变量），用来表示是否经嘌呤霉素处理，令x2=1表示经过处理，x2=0表示未经处理；参数β1是未经处理的最终反应速度，γ1是经处理后最终反应速度的增长值；β2是未经处理的反应的半速度点，γ2是经处理后反应的半速度点的增长值（为一般化起见，这里假定嘌呤霉素的处理也会影响半速度点）.

【混合模型的求解和分析】

仍用MATLAB统计工具箱中的命令nlinfit来计算模型（9.2.3）的回归系数β1，β2，γ1和γ2.为了给出合适的初始迭代值，从实验数据我们注意到，未经处理的反应速度的最大实验值为160，经处理的最大实验值为207，于是可取参数初值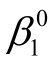=170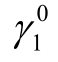，=60；又从数据可大致估计未经处理的半速度点约为0.05，经处理的半速度点约为0.06，我们取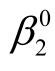=0.05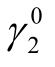，=0.0 1.

与模型（9.2.1）的编程计算相似，运行如下程序文件model4.m及建立M-函数“huaxue2”：

得到混合模型（9.2.3）的回归系数的估计值与其置信区间（见表9.2.4）、拟合结果（见图9.2.7）、残差图（见图9.2.8），及预测和结果输出图（见图9.2.9），模型的剩余标准差s=10.4000.

表9.2.4　模型（9.2.3）参数的估计结果

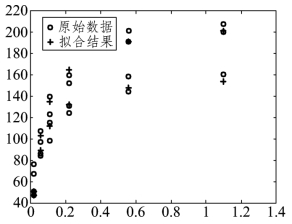
图9.2.7　模型（9.2.3）的预测图

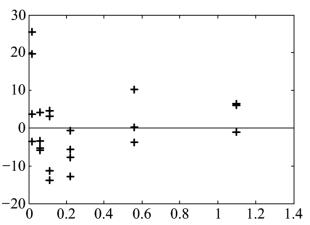
图9.2.8　模型（9.2.3）残差图

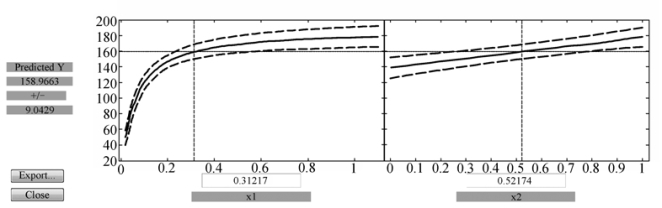
图9.2.9　模型（9.2.3）的预测及结果输出

然而，从表9.2.4可以发现，γ2的置信区间包含零点，这表明参数γ2对因变量y的影响并不显著，这一结果与前面的说法（即嘌呤霉素的作用不影响半速度参数）是一致的.因此，可以考虑简化模型：

采用与模型（9.2.3）类似的计算、分析方法，在上述程序文件model4.m中添加如下程序段并建立M-函数“huaxue3”：

运行得到的模型（9.2.4）的结果概括在表9.2.5和表9.2.6，以及图9.2.10、图9.2.11和图9.2.12中，模型（9.2.4）的剩余标准差s=10.5851.

表9.2.5　模型（9.2.4）参数的估计结果

表9.2.6　模型（9.2.3）与模型（9.2.4）预测值与预测区间的比较（预测区间为预测值±Δ）

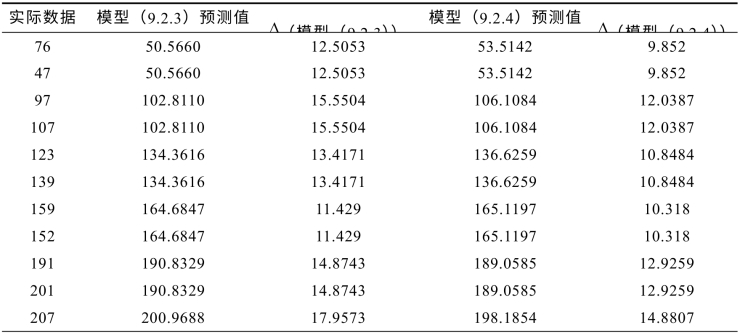
续表

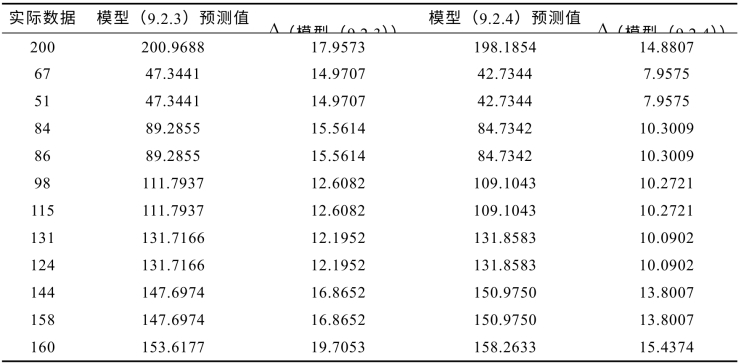
混合模型（9.2.3）和（9.2.4）不仅有类似于模型（9.2.1）的实际解释，同时把嘌呤霉素处理前后酶促反应速度之间的变化体现在模型之中，因此它们比单独的模型具有更实际的价值.另外，虽然模型（9.2.4）的某些统计指标可能没有模型（9.2.3）好，比如模型（9.2.4）的剩余标准差略大于模型（9.2.3），但由于它的形式更简单明了，易于实际中的操作和控制，而且从表9.2.6中数据可以发现，虽然两个模型的预测值相差不大，但模型（9.2.4）预测区间的长度明显比模型（9.2.3）短.因此，总体来说模型（9.2.4）更为优良.

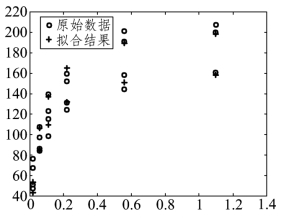
图9.2.10　模型（9.2.4）的预测图

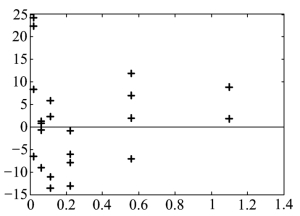
图9.2.11　模型（9.2.4）的残差图

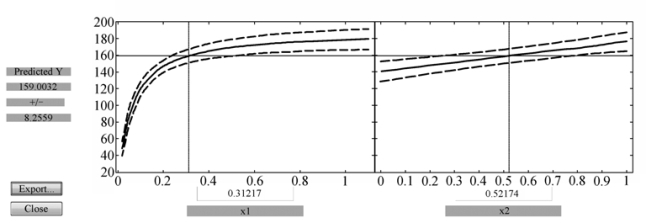
图9.2.12　模型（9.2.4）的预测及结果输出

评注：从实验数据看，酶促反应中反应速度与底物浓度及嘌呤霉素的作用之间的关系是非线性的，我们先用线性化模型来简化参数估计，如果能得到满意的结果，当然很好，但是由于变量的代换已经隐含了误差扰动项的变换，因此，除非变换后的误差项仍具有常数方差，一般情况下我们还需要用原始数据作非线性回归，而把线性化模型的参数估计结果作为非线性模型参数估计的迭代初值.应该指出，在非线性模型参数估计中，用不同的参数初值进行迭代，可能得到差别很大的结果（都是拟合误差平方和的局部极小点），也可能出现收敛速度问题，因此，合适的初值是非常重要的.

另外，评价线性回归模型拟合程度的统计检验无法直接用于非线性模型.例如，F统计量不能用于非线性模型拟合程度的显著性检验，因为即使误差项服从均值为0的正态分布，也无法从回归残差得到误差方差的一个无偏估计.但是R2和剩余标准差s仍然可以在通常意义下用于非线性回归模型拟合程度的度量.

从本例还可以看到，通过引入示性变量，能够描述定性上不同的处理水平对模型参数的影响，这是一种直接明了的建模方法.