某大型牙膏制造企业的销售量预测模型

某大型牙膏制造企业为了更好地拓展产品市场，有效地管理库存，公司董事会要求销售部门根据市场调查，找出公司生产的牙膏销售量与销售价格、广告投入等之间的关系，从而预测出在不同价格和广告费用下的销售量.为此，销售部的研究人员收集了过去30个销售周期（每个销售周期为4周）公司生产的牙膏的销售量、销售价格、投入的广告费用，以及同期其他厂家生产的同类牙膏的市场平均销售价格，如表9.1.1所示.试根据这些数据建立一个数学模型，分析牙膏销售量与其他因素的关系，以便为制订价格策略和广告投入策略提供数量依据[19].

表9.1.1　牙膏销售量与销售价格、广告费用等数据

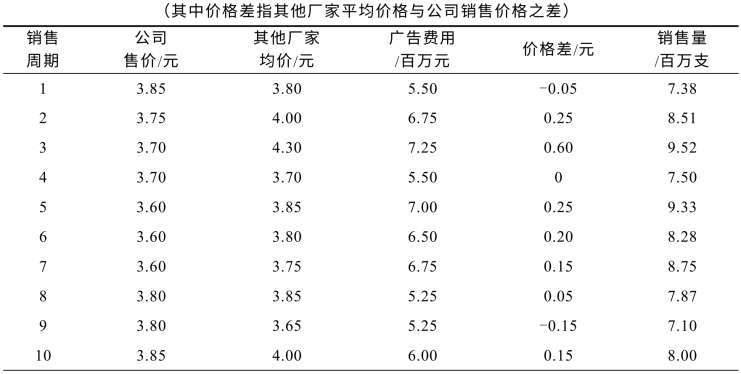
续表

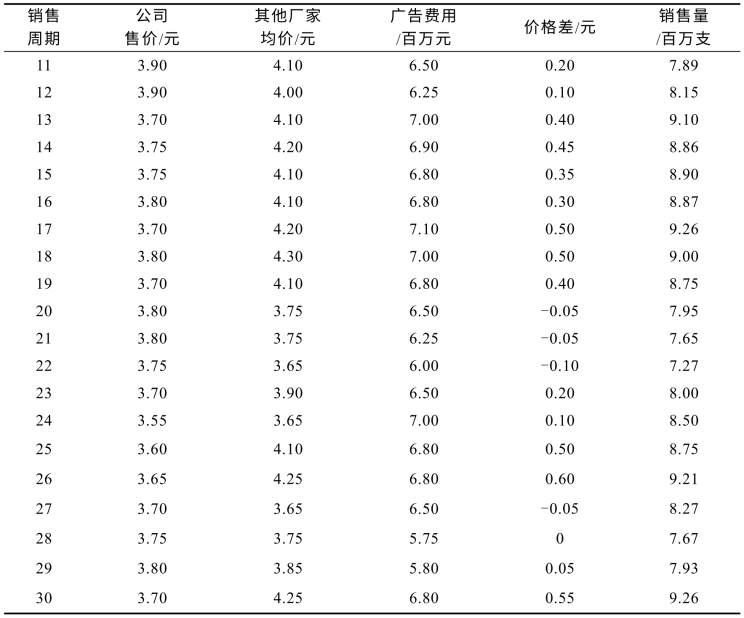
【分析与假设】

由于牙膏是生活必需品，对大多数顾客来说，在购买同类产品的牙膏时更多地会在意不同品牌之间的价格差异，而不是它们的价格本身.因此，在研究各个因素对销售量的影响时，用价格差代替公司的销售价格和其他厂家的平均价格更合适.

记牙膏销售量为y，其他厂家的平均价格与该公司的销售价格之差（价格差）为x1，公司投入的广告费用为x2，其他厂家的平均价格和该公司的销售价格分别为x3和x4，x1=x3-x4.基于上面的分析，我们仅利用x1和x2来建立y的预测模型.

【模型建立】

为了大致地分析y与x1和x2的关系，首先利用表9.1.1的数据在MATLAB中运行如下程序段1：

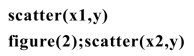
分别作出y对x1和x2的散点图（见图9.1.1和图9.1.2），并在图形窗口菜单选择Tools/Basic fitting，在弹出的对话框中分别勾选linear和quadratic.

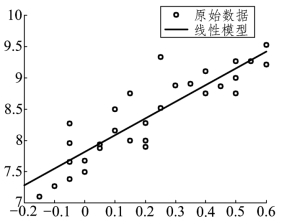
图9.1.1　y对x1的散点图

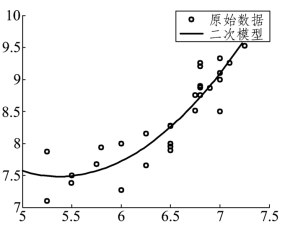
图9.1.2　y对x2的散点图

从图9.1.l可以发现，随着x1的增加，y的值有比较明显的线性增长趋势，图中的直线是用线性模型：

拟合的（其中ε是随机误差）.而在图9.1.2中，当x2增大时，y有向上弯曲增加的趋势，图中的曲线是用二次函数模型：

拟合的.

综合上面的分析，结合模型（9.1.1）和（9.1.2）建立如下的回归模型：

（9.1.3）式右端的x1和x2称为回归变量（自变量），是给定价格差x1、广告费用x2时，牙膏销售量y的平均值，其中参数β0，β1，β2，β3称为回归系数，由表9.1.1的数据估计，影响y的其他因素的作用都包含在随机误差ε中.如果模型选择合适，ε应大致服从均值为0的正态分布.

【模型求解】

直接利用MATLAB统计工具箱中的命令regress求解，使用格式为：

[b,bint,r,rint,stats]=regress(y,x,alpha)

其中输入y为模型（9.1.3）中y的数据（n维向量，n=30）；x为对应于回归系数β=(β0，β1，β2，β3)的数据矩阵（n×4矩阵，其中第1列为全1向量）；alpha为显著性水平α（缺省时α=0.05）；输出b为β的估计值，常记作ˆβ，bint为b的置信区间；r为残差向量，rint为r的置信区间；stats为回归模型的检验统计量，有四个值，第一个是回归方程的决定系数R2（R是相关系数），第二个是F统计量值，第三个是与F统计量对应的概率值p，第四个是剩余方差s2.

在上述程序段1基础上添加如下程序段2：

运行得到模型（9.1.3）的回归系数估计值及其置信区间（置信水平α=0.05）以及检验统计量R2，F，p，s2的结果（见表9.1.2）.

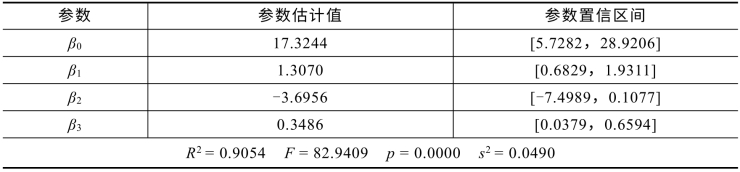
表9.1.2　模型（9.1.3）的计算结果

【结果分析】

表9.1.2显示，R2=0.9054指因变量y（销售量）的90.54%可由模型确定，F值远远超过F检验的临界值，p远小于α，因而模型（9.1.3）从整体来看是可用的.

表9.1.2的回归系数给出了模型（9.1.3）中β0，β1，β2，β3的估计值，即检查它们的置信区间发现，只有β2的置信区间包含零点（但区间右端点距零点很近），表明回归变量x2（对因变量y的影响）不是太显著，但由于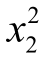是显著的，我们仍将变量x2保留在模型中.

【销售量预测】

将回归系数的估计值代入模型（9.1.3），即可预测公司未来某个销售周期牙膏的销售量y，预测值记作ˆy，得到模型（9.1.3）的预测方程：

只需知道该销售周期的价格差x1和投入的广告费用x2，就可以计算预测值ˆy.

值得注意的是，公司无法直接确定价格差x1，而只能制订公司该周期的牙膏售价x4，但是同期其他厂家的平均价格x3一般可以通过分析和预测当时的市场情况及原材料的价格变化等估计出.模型中引入价格差x1=x3-x4作为回归变量，而非x3，x4的好处在于，公司可以更灵活地来预测产品的销售量（或市场需求量），因为x3的值不是公司所能控制的.预测时只要调整x4达到设定的回归变量x1的值，比如公司计划在未来的某个销售周期中，维持产品的价格差为x1=0.2元，并投入x2=6.5百万元的广告费，则该周期牙膏销售量的估计值为

ŷ=17.3244+1.3070×0.2-3.6956×6.5+0.3486×6.52=8.2928百万支.

回归模型的一个重要应用是，对于给定的回归变量的取值，可以以一定的置信度预测因变量的取值范围.比如当x1=0.2，x2=6.5时可以算出牙膏销售量的置信度为95%的预测区间为[7.8230，8.7636].它表明在将来的某个销售周期中，如公司维持产品的价格差为0.2元，并投入650万元的广告费用，那么可以有95%的把握保证牙膏的销售量在7.823与8.7636百万支之间.实际操作时，预测上限可以用来作为库存管理的目标值，即公司可以生产（或库存）8.7636百万支牙膏来满足该销售周期顾客的需求；预测下限则可以用来较好地把握（或控制）公司的现金流，理由是公司对该周期销售7.823百万支牙膏十分自信，如果在该销售周期中公司将牙膏售价定为3.70元，且估计同期其他厂家的平均价格为3.90元，那么董事会可以有充分的依据知道公司的牙膏销售额应在7.823×3.7≈29百万元以上.

【模型改进】

模型（9.1.3）中回归变量x1和x2对因变量y的影响是相互独立的，即牙膏销售量y的均值与广告费用x2的二次关系由回归系数β2和β3确定，而不依赖于价格差x1.同样地，y的均值与x1的线性关系由回归系数β1确定，而不依赖于x2.根据直觉和经验可以猜想，x1和x2之间的交互作用会对y有影响，不妨简单地用x1，x2的乘积代表它们的交互作用，于是将模型（9.1.3）增加一项，得到：

在这个模型中，y的均值与x2的二次关系为，由系数β2，β3，β4确定，并依赖于价格差x1.(www.xing528.com)

下面让我们用表9.1.1的数据估计模型（9.1.5）的系数.在上述程序段1-2基础上继续添加如下程序段3：

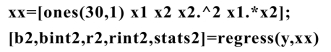
运行得到的结果如表9.1.3所示.

表9.1.3　模型（9.1.5）的计算结果

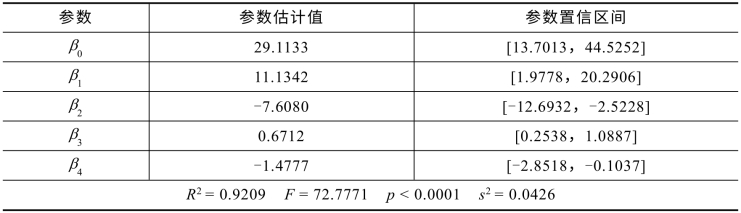
表9.1.3与表9.1.2的结果相比，R2有所提高，说明模型（9.1.5）比模型（9.1.3）有所改进.并且，所有参数的置信区间，特别是x1，x2的交互作用项x1x2的系数β4的置信区间不包含零点，所以有理由相信模型（9.1.5）比模型（9.1.3）更符合实际.

用模型（9.1.5）对公司的牙膏销售量作预测.仍设在某个销售周期中，维持产品的价格差x1=0.2元，并将投入x2=6.5百万元的广告费用，则该周期牙膏销售量y的估计值为

置信度为95%的预测区间为[7.8953，8.7592]，与模型（9.1.3）的结果相比，略有增加，而预测区间长度短一些.

在保持广告费用x2=6.5百万元不变的条件下，分别对模型（9.1.3）和（9.1.5）中牙膏销售量的均值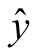与价格差x1的关系作图，为此，在上述程序段1-3基础上添加程序段4：

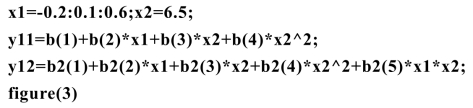
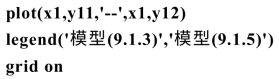
运行结果如图9.1.3所示.

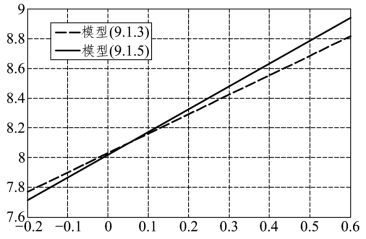
图9.1.3　模型（9.1.3）和（9.1.5）中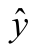与x1的关系

在保持价格差x1=0.2元不变的条件下，分别对模型（9.1.3）和（9.1.5）中牙膏销售量的均值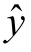与广告费用x2的关系作图，为此，在上述程序段1-4基础上添加程序段5：

运行结果如图9.1.4所示.

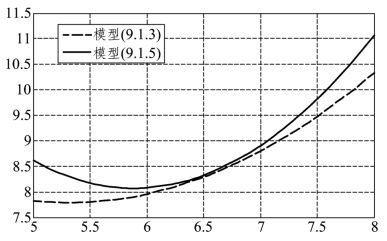
图9.1.4　模型（9.1.3）和（9.1.5）中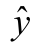与x2的关系

可以看出，将交互作用项x1x2加入模型，对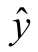与x1的关系稍有影响，而对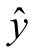与x2的关系影响较大，当x2＜6时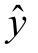出现下降，在x2＞6以后上升得很快.

【进一步讨论】

为进一步了解x1和x2之间的交互作用，考察（9.1.5）的预测方程：

如果取价格差x1=0.1元，代入（9.1.6）式可得

再取x1=0.3元，代入（9.1.6）式得

它们均为x2的二次函数，其图形如图9.1.5所示，且

由（9.1.9）式可得，当x2＜7.5360时，总有，即若广告费用不超过大约7.5百万元，价格差定在0.3元时的销售量，比价格差定在0.1元时要大，也就是说，这时的价格优势会使销售量增加.

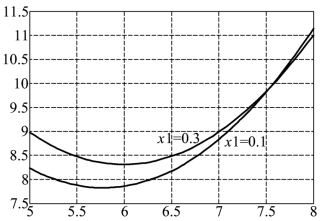
图9.1.5　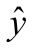与x2的关系图（（9.1.7）与（9.1.8）的图形）

由图9.1.5还可以发现，虽然广告投入的增加会使销售量增加（只要广告费用超过大约6百万元），但价格差较小时增加的速率要更大些.这些现象都是由于引入了交互作用项x1x2后产生的.价格差较大时，许多消费者是受价格的驱动来购买公司的产品，所以可以较少地依赖广告投入的增加来提高销售量；价格差较小时，则更需要靠广告来吸引更多的顾客.

另外，当公司牙膏的售价在市场中明显处于弱势时，x1和x2之间的交互作用项不见得就是乘积项x1x2了，可能出现其他形式的组合.

【完全二次多项式模型】

与x1和x2的完全二次多项式模型：

相比，模型（9.1.5）只少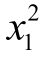项，我们不妨增加这一项，建立模型（9.1.10）.这样做的好处之一是MATLAB统计工具箱中有直接的命令rstool求解，并且以交互式画面给出y的估计值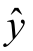和预测区间.运行如下程序段：

输出如图9.1.6所示，从左下方的输出Export可以得到模型（9.1.10）的回归系数的估计值为

β=(β0，β1，β2，β3，β4，β5)=(32.0984，14.7436，-8.6367，-2.1038，1.1074，0.7594).

用鼠标移动交互式画面中的十字线，或在图下方的窗口内输入，可改变x1和x2的数值，图中当x1=0.2，x2=6.5时，左边的窗口显示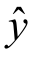=8.3029，预测区间为8.3029±0.2558=[8.0471，8.5587].这些结果与模型（9.1.5）相差不大.

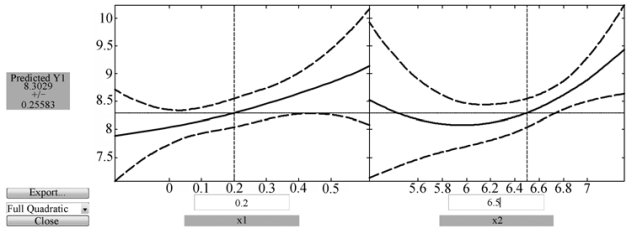
图9.1.6　完全二次多项式模型（9.1.10）的输出

评注：从这个实例可以看到，建立回归模型可以先根据已知的数据，从常识和经验进行分析，辅以作图（如图9.1.1，图9.1.2的散点图），决定取哪几个回归变量及它们的函数形式（如线性的、二次的）.用软件（如MATLAB统计工具箱）求解后，作统计分析：R2、F、p值、s2的大小是对模型整体的评价；每个回归系数置信区间是否包含零点，可以用来检验对应的回归变量对因变量的影响是否显著（若包含零点则不显著）.如果对结果不够满意，则应改进模型，如添加二次项、交互项等.

对因变量进行预测，经常是建立回归模型的主要目的之一，本节提供了预测的方法，以及对结果做进一步讨论的实例.