中学数学建模方法-旅行商问题的解决与最小总费用211

下面介绍旅行商问题（又称货郎担问题，Traveling Salesman Problem，简称TSP问题）.

有一个推销员，从城市1出发，要遍访城市2，3，…，n各一次，最后返回城市1.已知从城市i到j的旅程为cij，问他应按怎样的次序访问这些城市，才使得总旅程最短？用图论术语说，就是在一个赋权完全图中，找出一个有最小权的Hamilton圈，称这种圈为最优圈.

可以用多种方法把TSP表示成整数规划模型.这里介绍的一种建立模型的方法，是把该问题的每个解（不一定是最优的）看作一次“巡回”.

在下述意义下，引入一些0-1整数变量：

其目标是使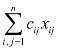为最小.

这里有两个明显的必须满足的条件：

（1）访问城市i后必须要有一个即将访问的确切城市；

（2）访问城市j前必须要有一个刚刚访问过的确切城市.

用下面的两组约束分别实现上述两个条件.

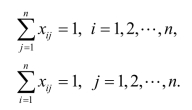
到此我们得到了一个模型，它是一个指派问题的整数规划模型.但以上两个条件对于TSP来说并不充分，仅仅是必要条件.例如，图8.4.1所示的双子巡回的情形.

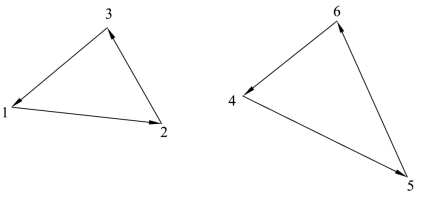
图8.4.1　双子巡回的情形

以上两个条件都满足，但它显然不是TSP的解，它存在两个子巡回.

这里，我们将叙述一种在原模型上附加充分的约束条件以避免产生子巡回的方法.把额外变量u i (i=2，3，…，n)附加到问题中，可把这些变量看作连续的（虽然这些变量在最优解中取普通的整数值），现在附加下面形式的约束条件：

为了证明该约束条件有预期的效果，必须证明：

（1）任何含子巡回的路线都不满足该约束条件；

（2）全部巡回都满足该约束条件.

首先证明（1），用反证法.假设还存在子巡回，也就是说至少有两个子巡回，那么至少存在一个子巡回不含城市1.把该子巡回记为i1 i 2…ik i1，则必有：(www.xing528.com)

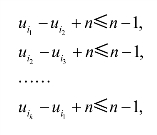
把这k个式子相加，有：

故假设不正确，结论（1）得证.

下面证明（2），采用构造法.对于任意的总巡回1i1 …in -11，可取

ui=访问城市i的顺序数，取值范围为{0，1，2，…，n-1}.

因此，u i-u j ≤n-2， 2≤i ≠j≤ n .下面证明总巡回满足该约束条件.

①总巡回上的边：

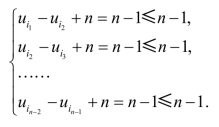
②非总巡回上的边：

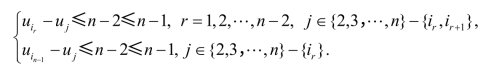
从而结论（2）得证.

这样我们把TSP转化成了一个混合整数线性规划问题：

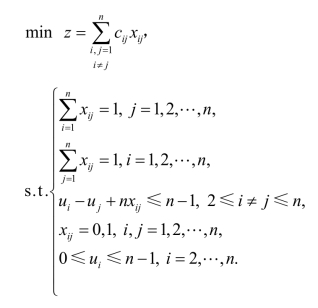
显然，当城市个数较多（大于30）时，该混合整数线性规划问题的规模会很大，从而给求解带来很大问题.TSP已被证明是NP难问题，目前还没有发现多项式时间的算法.对于小规模问题，我们求解这个混合整数线性规划问题的方式还是有效的.

例从北京（Pe）乘飞机到东京（T）、纽约（N）、墨西哥城（M）、伦敦（L）、巴黎（Pa）五城市旅游，每城市恰好去一次再回北京，应如何安排旅游线路，使旅费最省？各城市之间的机票价格如表8.4.1所示.

表8.4.1　城间旅游费用

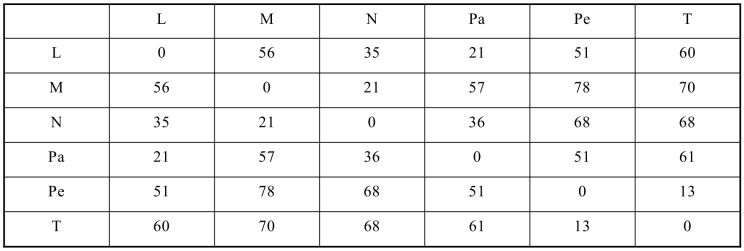
运行如下LINGO程序tsp.lg4

得到x14=x45=x56=x62=x23=x31=1，目标值为211，即从北京出发依次经过东京（T）、墨西哥城（M）、纽约（N）、伦敦（L）、巴黎（Pa），再回到北京，最小总费用211.