中学数学建模方法：图论基本概念

一、无向图

定义8.1一个无向图（undirected graph）G是由一个非空有限集合V (G)和V (G)中某些元素的无序对集合E (G)构成的二元组，记为G =(V (G )，E (G)).其中V (G)={v1 ，v2，…，vn }称为图G的顶点集（vertex set）或节点集（node set），V (G)中的每一个元素vi (i=1，2，…，n)称为该图的一个顶点（vertex）或节点（node）；E (G)={e1 ，e2，…，em }称为图G的边集（edge set），E (G)中的每一个元素ek（即V (G)中某两个元素vi ，vj 的无序对）记为ek=(v i，vj )或ek =vi v j=v j vi (k=1，2，…，m)，称为该图的一条从vi到vj的边（edge）.如果V (H)⊂V (G )，E (H)⊂E (G)，则称图H为图G的子图，记作H ⊂G.

当边ek =vi vj 时，称vi ，vj 为边ek的端点，并称vj与vi相邻（adjacent）；边ek称为与顶点vi ，vj 关联（incident）.G中与顶点v关联的边数称为v的度，记作d(v).如果某两条边至少有一个公共端点，则称这两条边相邻.

如果图的顶点集和边集都有限，则称为有限图.图G的顶点数用符号|V|或ν(G)表示，边数用|E|或ε(G)表示.

当讨论的图只有一个时，总是用G来表示这个图，从而在图论符号中常略去字母G，例如，分别用V ，E ，ν和ε代替V (G )，E (G)，ν(G)和ε(G).

端点重合为一点的边称为环（loop）.如果图既没有环也没有两条边连接同一对顶点，则称为简单图（simple graph）.

二、有向图

定义8.2　一个有向图（directed graph或digraph）G是由一个非空有限集合V和V中某些元素的有序对集合A构成的二元组，记为G =(V ，A).其中V={v1 ，v2，…，vn }称为图G的顶点集或节点集，V中的每一个元素vi (i=1，2，…，n)称为该图的一个顶点或节点；A ={a1 ，a2，…，am }称为图G的弧集（arc set），A中的每一个元素ak（即V中某两个元素vi ，vj 的有序对）记为ak=(vi ，vj )或a k=vi v j (k=1，2，…，n)，称为该图的一条从vi到vj的弧（arc）.

对应于每个有向图D，可以在相同顶点集上作一个图G，使得对于D的每条弧，G有一条有相同端点的边与之相对应，这个图称为D的基础图.反之，给定任意图G，对于它的每条边，给其端点指定一个顺序，从而确定一条弧，由此得到一个有向图，这样的有向图称为G的一个定向图.若将图G的每一条边e都对应一个实数w( e)，则称w( e)为边的权，并称图G为赋权图.

以下若未指明“有向图”三字，皆指无向图.

三、图的数据结构

为了在计算机上实现图论优化的算法，首先必须有一种在计算机上来描述图的方法（即数据结构）.一般来说，算法的好坏与图的具体表示方法，以及中间结果的操作方案是有关系的.这里介绍两种常用的在计算机上描述图的表示方法：邻接矩阵表示法、关联矩阵表示法.在下面的讨论中，首先假设G =(V ，A)是一个简单图，|V |=n，|A |=m.

1.邻接矩阵表示法

定义8.3　对无向图G =(V ，A)，其邻接矩阵（adjacency matrix）定义为A=(aij )n×n ，其中

对有向图G，其邻接矩阵定义为A=(aij )n×n ，其中

对赋权图G，其邻接矩阵定义为A=(aij )n×n ，其中

例1　对于图8.1.1所示的图，可以用邻接矩阵表示为(www.xing528.com)

图8.1.1

2.关联矩阵表示法

定义8.4无向图G =(V ，A)的关联矩阵（incidence matrix）B定义为B=(bij )n×m ，其中

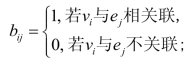
对有向图G，其关联矩阵定义为B=(bij )n×n ，其中

例2　对于图8.1.1，如果关联矩阵中每列对应弧的顺序为(1，2)，(1，3)，(2，4)，(3，2)，(4，3)，(4，5)，(5，3)和(5，4)，则关联矩阵表示为

对于图中的权，也可以通过扩展关联矩阵来表示.例如，如果图中每条弧有一个权，可以把关联矩阵增加一行，把每一条弧所对应的权存储在增加的行中.如果图中每条弧赋有多个权，可以把关联矩阵增加相应的行数，把每一条弧所对应的权存储在增加的行中.

四、轨与连通

定义8.5W =v 0 e1 v 1 e 2 …ek vk ，其中ei ∈E (G)，1≤i ≤k ，v j ∈V (G)，0≤j ≤k ，ei与v i-1，vi 关联，称W是图G的一条道路，k为路长，顶点v0和vk分别称为W的起点和终点，而v1 ，v2，…，vk -1称为它的内部顶点.

若道路W的边互不相同，则W称为迹（trail）.若道路W的顶点互不相同，则W称为轨（path）.

如果一条道路长为正数且起点和终点相同，则称这条道路是闭的.起点和终点重合的轨叫做圈（cycle）.

若图G的两个顶点u ，v间存在道路，则称u和v连通（connected）.u ，v间的最短轨的长叫做u ，v间的距离.记作d (u ，v).若图G的任意两顶点均连通，则称G是连通图.

显然有：

（1）图P是一条轨的充要条件是P是连通的，且有两个1度顶点，其余顶点为2度；

（2）图C是一个圈的充要条件是C是各顶点的度均为2的连通图.