合理分配效益-中学数学建模方法

在经济或社会活动中若干实体（如个人、公司、党派、国家等）相互合作结成联盟或集团，常能比他们单独行动获得更多的经济或社会效益.确定合理地分配这些效益的方案是促成合作的前提.先看一个简单例子.

引例甲乙丙三人经商，若单干，每人仅能获利1元；甲乙合作可获利7元；甲丙合作可获利5元；乙丙合作可获利4元；三人合作则可获利11元.问三人合作时怎样合理地分配11元的收入.

人们自然会想到的一种分配方法是：设甲、乙、丙三人各得x1，x2，x3元，满足：

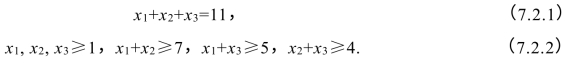
（7.2.2）式表示这种分配必须不小于单干或两人合作时的收入.但是容易看出，（7.2.1）式、（7.2.2）式有许多组解，如(x1，x2，x3)=(5，3，3)，(4，4，3)，(4，3.5，3.5)等，于是应该寻求一种圆满的分配方法.

引例提出的这类问题称为n人合作对策（Cooperative n-person Game）.1953年，L.S.Shapley给出了解决该问题的一种方法，称Shapley值[15，16].

一、n人合作对策和Shapley值

n个人从事某项经济活动，对于他们之中若干人组合的每一种合作（特别，单人也视为一种合作），都会得到一定的效益，当人们之间的利益是非对抗性时，合作中人数的增加不会引起效益的减少，这样，全体n个人的合作将带来最大效益.n个人的集合及各种合作的效益就构成n人合作对策，Shapley值是分配这个最大效益的一种方案.其定义如下：

设集合I={1，2，…，n}，如果对于I的任一子集s都对应着一个实值函数v(s)，满足：

称[I，v]为n人合作对策，v为对策的特征函数.

在上面所述的经济活动中，I定义为n人集合，s为n人集合中的任一种合作，v(s)为合作s的效益.

用xi表示I的成员i从合作的最大效益v(I)中应得到的一份收入，x =(x1 ，x2，…，xn )叫做合作对策的分配（imputation），满足：

显然，由（7.2.3），（7.2.4）式定义的n人合作对策[I，v]通常有无穷多种分配方法.

Shapley值由特征函数v确定，记作Φ(v)=(φ1(v)，φ2(v)，…，φn(v)).对于任意的子集s，记，即s中各成员的分配.对一切s I满足x(s)≥v(s)的x组成的集合称为[I，v]的核心（Core）.当核心存在时，即所有s的分配都不小于s的效益，可以将Shapley值作为一种特定的分配，即φi(v)=xi.

Shapley首先提出看来毫无疑义的几条公理，然后用逻辑推理的方法证明，存在唯一的满足这些公理的分配Φ(v)，并把它构造出来.这里只给出Φ(v)的结果，Shapley公理可参看[17，18].

Shapley值Φ(v)=(φ1(v)，φ2(v)，…，φn(v))为：

其中Si是I中包含i的所有子集，|s|是子集s中的元素数目（人数），w(|s|)是加权因子，s\i表示s去掉i后的集合.

我们用这组公式计算本节开始给出的三人经商问题的分配，以解释公式的用法.

甲、乙、丙三人记为I={1，2，3}，经商获利定义为I上的特征函数，即

v(∅)=0，v(1)=v(2)=v(3)=1，v(1，2)=7，v(1，3)=5，v(2，3)=4，v(I)=11.

容易验证，v满足（7.2.3），（7.2.4）式.为计算φ1(v)，首先找出I中包含1的所有子集S1:{1}，{1，2}，{1，3}，I，然后令s跑遍S1，将计算结果记入表7.2.1中.最后将表中末行相加得.同法可计算出.它们可作为按照Shapley值方法计算的甲、乙、丙三人应得的分配.

让我们通过此例对（7.2.7）式做些解释.对表7.2.1中的s，比如{1，2}，v(s)是有甲（即{1}）参加时合作s的获利，v(s\1)是无甲参加时合作s（只剩下乙）的获利，所以v(s)-v(s\1)可视为甲对这一合作的“贡献”.用Shapley值计算的甲的分配，是甲对他所参加的所有合作（S1）的贡献的加权平均值，加权因子取决于这个合作s的人数.通俗地说就是按照贡献取得报酬.

表7.2.1　三人经商中甲的分配φ1(v)的计算

Shapley值方法可以有效处理经济和社会合作活动中的利益分配问题.请看下面的例子.

例1（污水处理费用的合理分担）沿河有三城镇1，2和3，地理位置如图7.2.1所示.污水需处理后才能排入河中.三城镇既可以单独建立污水处理厂，也可以联合建厂，用管道将污水集中处理（污水应由河流的上游城镇向下游城镇输送）.用Q表示污水量（单位：t/s），L表示管道长度（单位：km），按照经验公式，建立处理厂的费用为P1=73Q0.712千元，铺设管道费用P2=0.66Q0.51L千元.已知三城镇污水量为Q1=5，Q2=3，Q3=5，L的数值如图7.2.1所示，试从节约总投资的角度为三城镇制订污水处理方案.如果联合建厂，各城镇如何分担费用[3]？

图7.2.1　三城镇地理位置示意图

三城镇污水处理共有以下五种方案，计算出投资费用以做比较.

（1）分别建厂.

投资分别为C(1)=73×50.712=230，C(2)=160，C(3)=230，总投资D1=C(1)+C(2)+C(3)=620.

（2）1，2合作，在城2建厂.

投资为C(1，2)=73×(5+3)0.712+0.66×50.51×20=350，总投资D2=C(1，2)+C(3)=580.

（3）2，3合作，在城3建厂.

投资为C(2，3)=73×(3+5)0.712+0.66×30.51×38=365，总投资D3=C(1)+C(2，3)=595.

（4）1，3合作，在城3建厂.

投资为C(1，3)=73×(5+5)0.712+0.66×50.51×58=463，这个费用超过了1，3分别建厂的费用C(1)+C(3)=460.合作没有效益，不可能实现.

（5）三城合作，在城3建厂.

总投资为D5=C(1，2，3)=73×(5+3+5)0.712+0.66×50.51×20+0.66×(5+3)0.51×38=556.

比较结果以D5=556千元最小，所以应选择联合建厂方案.下面的问题是如何分担费用D5.

总费用D5有三部分：

联合建厂费d1=73×(5+3+5)0.712=453；

城1至2的管道费d2=0.66×50.51×20=30；

城2至3的管道费d3=0.66×(5+3)0.51×38=73.城3提出，d1由三城按污水量比例5∶3∶5分担，d2，d3是为城1，2铺设的管道费，应由他们担负；城2同意，并提出d3由城1，2按污水量之比5∶3分担，d2则应由城1自己担负；城1提不出反对意见，但他们计算了一下按上述办法各城应分担的费用：

城3分担费用为；

城2分担费用为；

城1分担费用为.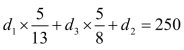

结果表明，城2，3分担的费用均比他们单独建厂费用C(2)，C(3)小，而城1分担的费用却比C(1)大.显然，城1不能同意这种分担总费用的办法.

为了促成三城联合建厂以节约总投资，应该寻求合理分担总费用的方案.三城的合作节约了投资，产生了效益，是一个n人合作对策问题，可以用Shapley值方法圆满地分配这个效益.

把分担费用转化为分配效益，就不会出现城1联合建厂分担的费用反而比单独建厂费用高的情况.将三城镇记为I={1，2，3}，联合建厂比单独建厂节约的投资定义为特征函数.于是有：

v(∅)=0，v(1)=v(2)=v(3)=0，

v(1，2)=C(1)+C(2)-C(1，2)=230+160-350=40，

v(2，3)=C(2)+C(3)-C(2，3)=160+230-365=25，

v(1，3)=0，

v(I)=C(1)+C(2)+C(3)-C(1，2，3)=230+160+230-556=64.

三城联合建厂的效益为64千元.用Shapley值作为这个效益的分配，城1应分得的份额的计算结果列入表7.2.2中，得到类似地算出可以验证看来，城2从总效益64千元中分配的份额最大，你能从城2的地理位置与合作对策的角度解释这个结果吗？

表7.2.2　污水处理问题中φ1(v)的计算

(www.xing528.com)

最后，在联合建厂方案总投资额556千元中各城的分担费用为：

城1：C(1)-=230-19.7=210.3；

城2：C(2)-=127.9；

城3：C(3)-=217.8.

二、Shapley值方法的缺点及其他解决办法

Shapley值方法以严格的公理为基础，在处理合作对策的分配问题时具有公正、合理等优点，但是它需要知道所有合作的获利，即要定义I={1，2，…，n}的所有子集（共2n个）的特征函数，这在实际上常常做不到.如n个单位合作治理污染，第i方单独治理的投资yi和n方合作治理的投资Y，通常是已知的，为了度量第i方在合作中的“贡献”，还要设法知道第i方不参加合作时其余n-1方所需的投资zi.特征函数应定义为合作的获利，即节约的投资，有

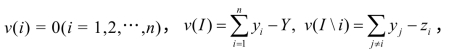
显然，除此之外还有许多v(s)不知道，无法用Shapley值方法求解.

下面仍以本节开始提出的三人经商问题为例，介绍几种其他解决办法.

我们只知道全体合作的获利，记作v(I)=B，及无i参加时其余n-1方合作的获利，记作v(I\i)=bi(i=1，2，…，n)，记b=(b1，b2，…，bn).确定各方对全体合作获利的分配，记作x =(x1 ，x2，…，xn ).三人经商问题中B=11，b=(4，5，7)，求x=(x1，x2，x3).

（1）协商解.

分配按以下两步进行.先从n个n-1方合作的获利得出各方分配的下限，即求解：

得到：

再计算按下限分配后全体合作获利的剩余为，它通常是较小的部分，经协商将其平均分配.于是最终的分配结果为

剩余，它等价于，请读者考察这个假定的含义.

对三人经商问题，

（2）均衡解.

设各方能够接受的现状点为d=(d1，d2，…，dn)，可看作谈判时的威慑点，在此基础上均衡地分配全体合作的获利B.根据n个数的和一定，当它们相等时乘积最大的原理，该模型为：

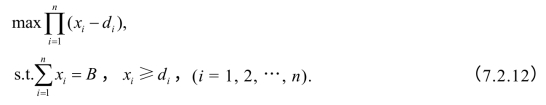
得到：

d=0时，相当于各方平均分配B；时，均衡解等价于协商解.

（3）最小距离解.

设存在一个各方理想的分配上限，记作，追求分配结果与这个上限的距离最小，模型为

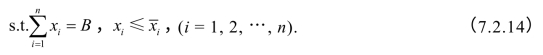
得到：

i方的理想上限若取为，看作i方对全体合作的“贡献”或i方的边际效益，将其代入（7.2.15）式可得，与（7.2.11）式相同，即最小距离解等价于协商解.对三人经商问题，

（4）满意解.

i方分配的满意度定义为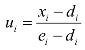，其中di是现状点，ei是理想点.为追求各方的满意度最高，用最小最大模型：

得到：

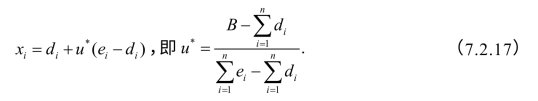
可以验证，当时，满意解等价于协商解.当时，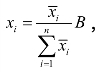

即按照各方理想上限的比例进行分配.

（5）Raiffa解.

Howard Raiffa提出的解决办法按以下步骤进行：

①按照n个n-1方合作的获利得到各方分配的下限，即协商解中的（见（7.2.10）式）作为分配的基础；

②当j方加入（原来无j的）n-1方合作时计算获利的增加，即j方的边际效益，是最小距离解中的上限

③按两步分配：先由j方和无j的n-1方平分，然后n-1方再等分，即

其中n-1方是在的基础上分配；

④j取1，2，…，n，重复第③步，然后求和、平均，得到最终分配结果：

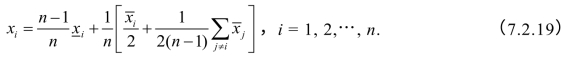
将代入，（7.2.19）式又可表为

对三人经商问题，

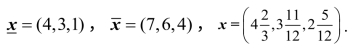
（6）几种方法的比较.

上面介绍的方法中，协商解、均衡解、最小距离解和满意解比较简单，容易理解，并且在许多情况下是等价的，不妨并为一类.这样，连同Shapley值方法我们共讨论了三类方法：Shapley值方法；协商解等；Raiffa解.下面结合一个较为极端的例子说明它们的特点.

例　有一资方（甲）和两劳方（乙、丙），当且仅当资方与至少一劳方合作时才获利10元，应如何分配该获利？

解　甲、乙、丙三方记作1，2，3.

①Shapley值方法：特征函数定义为获利，则子集{l，2}，{1，3}，{l，2，3}的特征函数为10，其余均为0，容易算出Shapley值，将其作为一种分配，即得

②协商解等：由B=10，b=(0，10，10)得到于是x=(10，0，0).

③Raiffa解：将代入（7.2.19）式，即得

三种方法得到的结果不同，协商解等显然对劳方不公平，Raiffa解在一定程度上照顾了劳方的利益.

一般地，这三类方法有以下特点：Shapley值方法公正、合理，但是需要的信息太多，n较大时难以提供.协商解等计算简单，便于理解，但通常偏袒强者，可用于各方实力相差不大的情况.Raiffa解考虑了分配的上、下限，又吸取了Shapley的思想，在一定程度上保护了弱者.