公平的席位分配方法-中学数学建模方法

某学校有3个系共200名学生，其中甲系100名，乙系60名，丙系40名.若学生代表会议设20个席位，公平而又简单的席位分配办法是按学生人数的比例分配，显然，甲、乙、丙三系分别应占有10，6，4个席位.

现在丙系有6名学生转入甲、乙两系，各系人数如表7.1.1第2列所示，仍按比例（表7.1.1第3列）分配席位时出现了小数（表7.1.1第4列）.在将取得整数的19席分配完毕后，三系同意参照所谓惯例分给比例分配中小数部分最大的丙系，于是三系仍分别占有10，6，4席（表7.1.1第5列）.

因为有20个席位的代表会议在表决提案时可能出现10∶10的局面，会议决定下一届增加1席.他们按照上述办法重新分配席位，计算结果见表7.1.1第6、7列.显然，这个结果对丙系太不公平了，因为总席位增加1席，而丙系却由4席减为3席.

表7.1.1　按照比例+惯例的席位分配

看来问题出在所谓按照惯例分配上.实际上，由A.Hamilton提出的这种办法在美国国会1850—1900年的众议员席位分配（按照人口比例每个州应分得几个席位）中就多次被采用，同时也被质疑[3，12]，称之为最大剩余法（GR：Greatest Remainders）或最大分数法（LF：Largest Fractions），也称为Hamilton法或Vinton法.它被质疑的一个理由就是上例出现的所谓席位悖论——总席位增加反而可能导致某州席位的减少.1880年，美国众议员席位分配时在亚拉巴马（Alabama）州就曾遇到这种情况，所以这个悖论又称亚拉巴马悖论.

最大剩余法的另一个重大缺陷就是所谓的人口悖论——某州人口增加较多反而可能导致该州席位的减少.如上例，若三系学生变为114，64，34名，按照最大剩余法21席的分配结果将是11，6，4席，然而乙系学生人数增加了席位反而比原来少了1席，而丙系学生数量未变席位反而多了1席.

为了寻求新的、公平的席位分配方法，下面先讨论衡量公平的数量指标[13，14].

不公平度指标　为简单起见，考虑A，B两方分配席位的情况.设两方人数分别为p1，p2，占有席位分别为n1，n2，则比值为两方每个席位所代表的人数.显然，仅当时分配才是完全公平的，但是因为人数和席位都是整数，所以通常，即分配不公平，并且是对比值较大的一方不公平.

不妨设，不公平程度可用数值衡量.如设p1=120，p2=100，n1=n2=10，则=12-10=2.它衡量不公平的绝对程度，但常常无法区分不公平程度明显不同的情况.如当双方人数增至p1=1 020，p2=1 000，而n1，n2不变时，=102-100=2，即不公平的绝对程度不变，但是常识告诉我们，后面这种情况的不公平程度比起前面来已经大为改善了.

为了改进上述的绝对标准，自然会想到用相对标准.仍设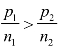，定义

为对A的相对不公平度；若，定义

为对B的相对不公平度.

建立了衡量不公平程度的指标rA，rB后，制订席位分配的原则是使它们尽可能地小.

新的分配方法假设A，B两方已分别占有席位n1，n2，利用相对不公平度rA，rB讨论当总席位增加1席时，应该分配给A还是分配给B呢？

不失一般性，可设，大于号成立时对A不公平.若增加的1席分配给A，n1就变为n1+1，若分配给B就有n2+1，原不等式可能出现以下三种情况（只需讨论不等号的情况，一旦等号出现，按等式状况分配即可）：

（1），说明即使A增加1席仍对A不公平.这一席显然应分配给A.

（2），说明A增加1席将对B不公平，参照（7.1.2）式计算出对B的相对不公平度为

（3），说明B增加1席将对A不公平，参照（7.1.1）式计算出对A的相对不公平度为

（不可能出现的情况）.(www.xing528.com)

在使相对不公平度尽量小的分配原则下，如果

则增加的1席应分配给A，反之，则增加的1席应分配给B（为等号时可分给任一方）.根据（7.1.3），（7.1.4）两式，（7.1.5）式等价于：

不难证明，上述第一种情况也会导致（7.1.6）式出现.于是我们的结论是：当（7.1.6）式成立时增加的1席应分配给A，反之应分配给B.

这种方法可推广到有m方分配席位的情况.设第i方人数为pi，已占有ni个席位，i=1，2，…，m，当总席位增加1席时，计算

增加的1席应分配给Q值最大的一方，此方法暂称为Q值法.

下面用Q值法重新讨论本节开头提出的甲、乙、丙三系分配21个席位的问题.

对本例，用Q值法可以从n1=n2=n3=1开始按总席位每增1席计算，直到19席的分配结果是n1=10，n2=6，n3=3，这与用最大剩余法得到的整数部分相同.再计算每次增加l席时的席位.

第20席：，Q1最大，增加的1席应分配给甲系.

第21席：，Q2，Q3同上，Q3最大，增加的1席应分配给丙系.

这样，21个席位的分配结果是三系分别占有11，6，4席，看来丙系保住了按照最大剩余法分配将会失掉的l席，可是，如果你注意一下上面的计算过程就会发现，当总席位是20席时，结果为11，6，3席，与最大剩余法的10，6，4席不同，所以很难说这个方法对丙系有利还是不利.

虽然从对这个具体问题的不同分配结果看，难以对Q值法与最大剩余法进行评判，但是Q值法不仅有明确的不公平度指标，而且由于它是在每次增加1席的情况下计算Q值的，所以不会出现席位悖论（也可证明不会出现人口悖论）.实际上，这个方法是20世纪20年代由哈佛大学数学家E.V.Huntington提出和推荐的一系列席位分配方法中的一个[3，13].

存在公平的席位分配方法吗约两个世纪以来，出于美国和欧洲诸如议会席位分配等社会政治活动的需要，一些人包括数学家们先后提出了许多分配方法，这些方法对同一个问题常常给出不同的结果，还会出现违反人们意愿甚至违背常识的现象，这更引起数学家们深入研究的兴趣.所谓公理化方法就是先提出公平的席位分配应该具有的若干性质，再找出满足这些性质的分配方法.如果不存在这样的方法，那就讨论现有的方法分别满足其中的哪些，再做改进，使之满足更多的性质；或者改变、减少原来提出的性质，再做探寻.

设第i方人数为pi，记p=(p1，p2，…，pm)，ni=fi(p，s)表示人数为p、总席位为s时分给第i方的席位，i=1，2，…，m.作为初步的、简明的介绍，这里只给出公平的席位分配明显应该具备的三条主要性质：

（1），其中，即ni必是精确的席位份额qi向下或向上取整得到的，称为份额性.

（2）fi(p，s)≤fi(p，s+1)，即总席位增加时各方的席位都不会减少，称为席位单调性.

（3）若对于任意的i，j=1，2，…，m，j≠i，，则

fi(p′，s)≥fi(p，s)或fj(p′，s)≤fj(p，s)，

即当i方相对于j方人数增加时（总席位不变），不会导致i方席位减少而j方席位增加（不排除i，j两方席位都增加或都减少），称为人口单调性.

我们已经看到，最大剩余法满足性质（1），但会出现席位悖论和人口悖论，从而不满足性质（2），（3）.而对于Q值法，从递推计算过程可知，它们自然满足性质（2），（3），那么是否能满足性质（1）呢？可以给出例子说明它不满足性质（1）（如，p=(91490，1660，1460，1450，1440，1400，1100)，s=100）.

是否存在满足所有三条性质的分配方法呢？事实上已经证明[13].对于m≥4，N≥m+3时，不存在满足上述三条性质的分配方法.

评注：起初，对于出现在社会政治领域中的席位分配，人们认为这是一个简单的数学问题，用初等的方法处理即可，但是在应用过程中发现，这样的分配方案会得出许多难以接受的结果，同时人们也发现所有的方法都有不合理之处.直到20世纪70年代，Balinski和Young采用公理化方法进行研究，才使解决这一问题的基本原理得以明晰.当然，这个问题还远未解决.