数学规划解决钢管下料问题

生产中常会遇到通过切割、剪裁、冲压等手段，将原材料加工成所需尺寸这种工艺过程，称为原料下料问题.按照进一步的工艺要求，确定下料方案，使用料最省或利润最大，是典型的优化问题.本节讨论用数学规划模型解决这类问题的方法.

钢管下料　某钢管零售商从钢管厂进货，将钢管按照顾客的要求切割后售出，从钢管厂进货时得到的原料钢管都是19 m.

（1）现有一客户需要50根4 m、20根6 m和15根8 m的钢管，应如何下料最节省？

（2）零售商如果采用的不同切割模式太多，将会导致生产过程复杂化，从而增加生产和管理成本，所以该零售商规定采用的不同切割模式不能超过3种.此外，该客户除需要（1）中的3种钢管外，还需要10根5 m的钢管.应如何下料最节省[8]？

问题（1）的求解

【问题分析】

首先，应当确定哪些切割模式是可行的.所谓一个切割模式，是指按照客户需要在原料钢管上安排切割的一种组合.例如，我们可以将19 m的钢管切割成3根4 m的钢管，余料为7 m；或者将19 m的钢管切割成4 m、6 m和8 m的钢管各1根，余料为1 m.显然，可行的切割模式是很多的.

其次，应当确定哪些切割模式是合理的.通常假设一个合理的切割模式的余料不应该大于或等于客户需要的钢管的最小尺寸.例如，将19 m的钢管切割成3根4 m的钢管是可行的，但余料为7 m，可以进一步将7 m的余料切割成4 m钢管（余料为3 m），或者将7 m的余料切割成6 m钢管（余料为1 m）.

求1根19 m的钢管切割为4 m、6 m、8 m的钢管的所有模式相当于求解不等式：

4k1+6k2+8k3≤19

的整数解.但要求剩余材料r=19-(4k1+6k2+8k3)＜4.使用穷举法编写MATLAB程序如下：

运行程序求得切割模式一共有7种，如表5.5.1所示.

表5.5.1　钢管下料的合理切割模式

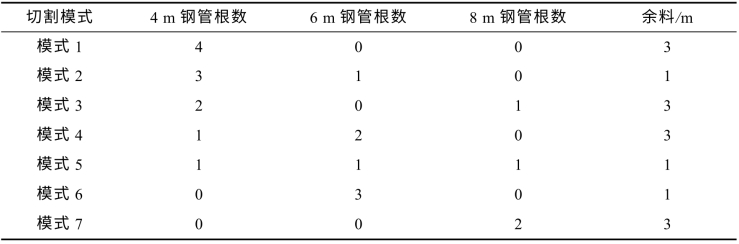
问题化为在满足客户需要的条件下，按照哪些合理的模式，切割多少根原料钢管，最为节省.而所谓节省，可以有两种标准：一是切割后剩余的总余料量最小；二是切割原料钢管的总根数最少.下面将对这两个目标分别讨论.

【模型建立】

决策变量：用xi表示按照第i种模式(i=1，2，…，7)切割的原料钢管的根数，显然它们应当是非负整数.

目标函数：以切割后剩余的总余料量最小为目标，则由表5.5.1可得

以切割原料钢管的总根数最少为目标，则有

下面分别在这两种目标下求解.

约束条件：为满足客户的需求，按照表5.5.1应有：

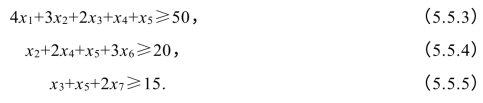
【模型求解】(www.xing528.com)

（1）将（5.5.1），（5.5.3），（5.5.4），（5.5.5）构成的整数线性规划模型（加上整数约束）输入LINGO求解，可以得到最优解为：x2=12，x5=15（其余变量为0）.即按照模式2切割12根原料钢管，按照模式5切割15根原料钢管，共27根，总余料量为27 m.显然，在总余料量最小的目标下，最优解将是使用余料尽可能小的切割模式（模式2和5的余料为1 m），这会导致切割原料钢管的总根数较多.

（2）将（5.5.2）～（5.5.5）构成的整数线性规划模型（加上整数约束）输入LINGO求解，可以得到最优解为：x2=15，x5=x7=5（其余变量为0）.即按照模式2切割15根原料钢管、按照模式5切割5根、按照模式7切割5根，共25根，可算出总余料量为35 m.与上面得到的结果相比，总余料量增加了8 m，但是所用的原料钢管的总根数减少了2根.在余料没有什么用途的情况下，通常选择总根数最少为目标.

问题（2）的求解

【问题分析】

按照问题（1）的思路，可以通过穷举法首先确定哪些切割模式是可行的.但由于需求的钢管规格增加到4种，所以用穷举法计算的工作量较大.下面介绍的整数非线性规划模型，可以同时确定切割模式和切割计划，是带有普遍性的方法.

同问题（1）类似，一个合理的切割模式的余料不应该大于或等于客户需要的钢管的最小尺寸（本题中为4 m），切割计划中只使用合理的切割模式，而由于本题中参数都是整数，所以合理的切割模式的余量不能大于3 m.此外，这里仅选择总根数最少为目标进行求解.

【模型建立】

决策变量：由于不同切割模式不能超过3种，可以用xi表示按照第i种模式(i=1，2，3)切割的原料钢管的根数，显然它们应当是非负整数.设所使用的第i种切割模式下每根原料钢管生产4 m、5 m、6 m和8 m的钢管数量分别为r1i，r2i，r3i，r4i(非负整数).

目标函数：切割原料钢管的总根数最少，目标为

约束条件：为满足客户的需求，应有

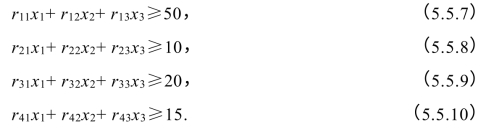
每一种切割模式必须可行、合理，所以每根原料钢管的成品量不能超过19m，也不能少于16 m（余量不能大于3 m），于是

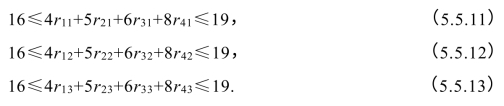
【模型求解】

在（5.5.7）～（5.5.10）式中出现决策变量的乘积，是一个整数非线性规划模型，虽然用LINGO软件可以直接求解，但也可以增加一些显然的约束条件，从而缩小可行解的搜索范围，有可能减少运行时间.

例如，由于3种切割模式的排列顺序是无关紧要的，所以不妨增加以下约束：

又例如，我们注意到所需原料钢管的总根数有着明显的上界和下界.首先，无论如何，原料钢管的总根数不可能少于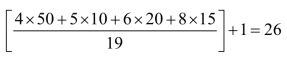根.其次，考虑一种非常特殊的生产计划：第一种切割模式下只生产4 m钢管，一根原料钢管切割成4根4 m钢管，为满足50根4 m钢管的需求，需要13根原料钢管；第二种切割模式下只生产5 m、6 m钢管，一根原料钢管切割成1根5 m钢管和2根6 m钢管，为满足10根5 m和20根6 m钢管的需求，需要10根原料钢管；第三种切割模式下只生产8 m钢管，一根原料钢管切割成2根8 m钢管，为满足15根8 m钢管的需求，需要8根原料钢管.于是满足要求的这种生产计划共需13+10+8=31根原料钢管，这就得到了最优解的一个上界.所以可增加以下约束：

将（5.5.6）～（5.5.15）构成的模型输入LINGO如下：

打开全局求解器求解可得到如下输出（只列出需要的结果）：

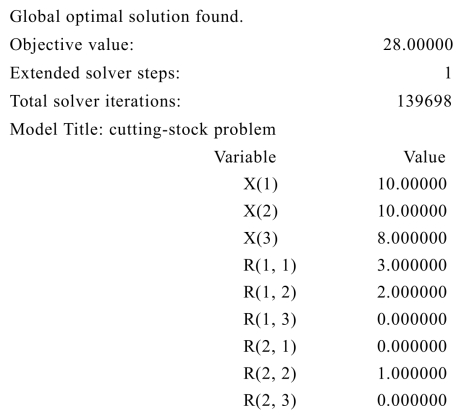
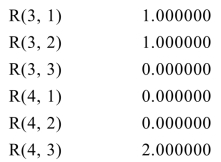
即按照模式1，2，3分别切割10，10，8根原料钢管，使用原料钢管总根数为28根.第一种切割模式下一根原料钢管切割成3根4 m钢管和1根6 m钢管；第二种切割模式下一根原料钢管切割成2根4 m钢管、1根5 m钢管和1根6 m钢管；第三种切割模式下一根原料钢管切割成2根8 m钢管.但这个模型的解并不唯一，你能找出一个与此不同的解吗？