中学生数学建模的接力队选拔和选课策略

实际生活中可能遇到这样的分派问题：若干项任务分给一些候选人来完成，因为每个人的专长不同，他们完成每项任务取得的效益或需要的资源也不一样，如何分派这些任务使获得的总效益最大，或付出的总资源最少？也会遇到这样的选择问题：有若干种策略供你选择，不同的策略得到的收益或付出的成本不同，各种策略之间可以有相互制约关系，如何在满足一定条件下作出最佳抉择，使得收益最大或成本最小？本节将通过几个实例说明怎样用数学规划模型解决这类问题.

一、混合泳接力队的选拔

某班准备从5名游泳队员中选择4人组成接力队，参加学校的4×100 m混合泳接力比赛.5名队员4种泳姿的百米平均成绩如表5.4.1所示，问应如何选拔队员组成接力队？

表5.4.1　5名队员4种泳姿的百米平均成绩

如果近期队员丁的蛙泳成绩有较大退步，只有1′15″2，而队员戊经过刻苦训练自由泳成绩有所进步，达到57''5，组成接力队的方案是否应该调整？

【问题分析】

从5名队员中选出4人组成接力队，每人一种泳姿，且4人的泳姿各不相同，使接力队的成绩最好，容易想到的一个办法是穷举法，组成接力队的方案共有5!=120种，逐一计算并作比较，即可找出最优方案.显然，这不是解决这类问题的好办法，随着问题规模的变大，穷举法的计算量将是无法接受的.可以用0-1变量表示一个队员是否入选接力队，从而建立此问题的0-1规划模型，借助现成的数学软件求解.

【模型的建立与求解】

记甲、乙、丙、丁、戊分别为队员i=1，2，3，4，5；记蝶泳、仰泳、蛙泳、自由泳分别为泳姿j=1，2，3，4.记队员i的第j种泳姿的百米最好成绩为tij(s)，数据预处理结果如表5.4.2所示.

表5.4.2　5名队员4种泳姿的百米平均成绩预处理结果

引入0-1变量xij，若选择队员i参加泳姿j的比赛，记xij=1，否则记xij=0.根据组成接力队的要求，xij应该满足下面两个约束条件：

第一，每人最多只能入选4种泳姿之一，即对于i=1，2，3，4，5，应有；

第二，每种泳姿必须有且只有1人入选，即对于j=1，2，3，4，应有；

当队员i入选泳姿j时，tijxij表示他（她）的成绩，否则tijxij=0.于是，接力队的成绩可表示为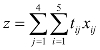，这就是该问题的目标函数.

综上，这个问题的0-1规划模型可写作：

利用题目所给数据，将这一模型输入LINGO：

求解得到结果为：x14=x21=x32=x43=1，其他变量为0，成绩为253.2 s=4′13″2.即应当选派甲、乙、丙、丁4人组成接力队，分别参加自由泳、蝶泳、仰泳、蛙泳的比赛.

【讨论】

考虑到丁、戊最近的状态，t43由原来的69.6 s变为75.2 s，t54由原来的62.4 s变为57.5 s，讨论对结果的影响.这类似于第五章第一节中的敏感性分析，但是对于整数规划模型，一般没有与线性规划相类似的理论，此时LINGO中所输出的敏感性分析结果通常是没有意义的.于是我们只好用t43，t54的新数据重新输入模型，用LINGO求解得到：x21=x32=x43=x54=1，其他变量为0，成绩为257.7 s=4′17″7.即应当选派乙、丙、丁、戊4人组成接力队，分别参加蝶泳、仰泳、蛙泳、自由泳的比赛.

评注：本例属于这样一类分派问题：有若干项任务，每项任务必须有一人且只能有一人承担，每人也只能承担其中一项，不同人员承担不同任务的收益（或成本）不同，问题是怎样分派各项任务才能使总收益最大（或总成本最小）.它又称为指派问题（assignment）.建立0-1规划模型是解决这类问题的常用方法.典型的指派问题中，任务的数量与能够承担的人员数量相等，但是两者不相等的情况也常见，本例是人数多于任务数，如果任务数多于人数呢？（这时虽然不是上述意义上的分派问题，但也能建立类似的模型）

二、选课策略

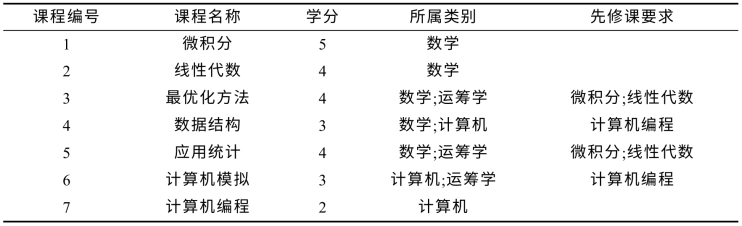
某学校规定，运筹学专业的学生毕业时必须至少学习过两门数学课、三门运筹学课和两门计算机课.这些课程的编号、名称、学分、所属类别和先修课要求如表5.4.3所示.那么，毕业时学生最少可以学习这些课程中的哪些课程？

表5.4.3　课程情况

如果某个学生既希望选修课程的数量少，又希望所获得的学分多，他可以选哪些课程？(www.xing528.com)

【模型的建立与求解】

用xi=1表示选修表5.4.3中按编号顺序的9门课程（xi=0表示不选；i=1，2，…，9）.问题的目标为选修的课程总数最少，即

约束条件包括下述两个方面：

第一，每人最少要学习2门数学课、3门运筹学课和2门计算机课.根据表5.4.3中对每门课程所属类别的划分，这一约束可以表示为：

第二，某些课程有先修课程的要求.例如，“数据结构”的先修课是“计算机编程”，这意味着如果x4=1，必须x7=1，这个条件可以表示为x4≤x7（注意：x4=0时对x7没有限制）.“最优化方法”的先修课是“微积分”和“线性代数”的条件可表为x3≤x1，x3≤x2，而这两个不等式可以用一个约束表示为2x3-x1-x2≤0.这样，所有课程的先修课要求可表为如下的约束：

由上得到以（5.4.5）为目标函数、以（5.4.6）～（5.4.14）为约束条件的0-1规划模型.将这一模型输入LINGO（注意加上xi为0-1的约束），求解得到结果为x1=x2=x3=x6=x7=x9=1，其他变量为0对照课程编号，它们是微积分、线性代数、最优化方法、计算机模拟、计算机编程、数学实验，共6门课程，总学分为21.

下面将会看到，这个解并不唯一的，还可以找到与以上不完全相同的6门课程，也满足所给的约束.

【讨论】

如果一个学生既希望选修课程数少，又希望所获得的学分数尽可能多，则除了目标（5.4.5）之外，还应根据表5.4.3中的学分数写出另一个目标，即

我们把只有一个优化目标的规划问题称为单目标规划，而将多于一个目标的规划问题称为多目标规划.多目标规划的目标函数相当于一个向量，如目标（5.4.5）和（5.4.15）可以表示为对一个向量进行优化：

上面符号“V-min”是“向量最小化”的意思，注意其中已经通过对w取负号而将（5.4.15）中的最大化变成了最小化问题.

要得到多目标规划问题的解，通常需要知道决策者对每个目标的重视程度，称为偏好程度.下面通过几个例子讨论处理这类问题的方法.

（1）同学甲只考虑获得尽可能多的学分，而不管所修课程的多少，那么他可以以（5.4.15）为目标，不用考虑（5.4.5），这就变成了一个单目标优化问题.显然，这个问题不必计算就知道最优解是选修所有9门课程.

（2）同学乙认为选修课程数最少是基本的前提，那么他可以只考虑目标（5.4.5）而不管（5.4.15），这就是前面得到的，最少为6门.如果这个解是唯一的，则他已别无选择，只能选修上面的6门课，总学分为21.但是LINGO无法告诉我们一个优化问题的解是否唯一，所以他还可能在选修6门课的条件下，使总学分多于21.为探索这种可能，应在上面的规划问题中增加约束：

得到以（5.4.15）为目标函数、以（5.4.6）～（5.4.14）和（5.4.17）为约束条件的另一个0-1规划模型.求解后发现会得到不同于前面6门课程的最优解x1=x2=x3=x5=x7=x9=1，其他变量为0，即3学分的“计算机模拟”换成了4学分的“应用统计”，总学分由21增至22.注意这个模型的解仍然不是唯一的，如x1=x2=x3=x5=x6=x7=1，其他变量为0，也是最优解.

（3）同学丙不像甲、乙那样，只考虑学分最多或以课程最少为前提，而是觉得学分数和课程数这两个目标大致上应该三七开.这时可以将目标函数z和-w分别乘以0.7和0.3，组成一个新的目标函数y，有

得到以（5.4.18）为目标、以（5.4.6）～（5.4.14）为约束的0-1规划模型.输入LINGO求解得到结果为：x1=x2=x3=x4=x5=x6=x7=x9=1，即只有“预测理论”不需要选修，共28学分.

实际上，0.7和0.3是z和-w的权重.一般地，将权重记作λ1，λ2，且λ1+λ2=1，0≤λ1，λ2≤1，则0-1规划模型的新目标为

前面同学甲的考虑相当于λ1=0，λ2=1，同学乙的考虑相当于λ1=1，λ2=0，是两种极端情况.通过选取许多不同的λ1，λ2进行计算，可以发现，当时，结果与同学甲相同；而当时，结果与同学乙相同.这是偶然的吗？我们根据给出的数据分析一下.

当时，（5.4.19）式中z的所有系数都小于0，因此为了使y取最小值，所有决策变量应尽可能取1，这与λ1=0，λ2=1的情况，即学分数最多是一样的.

当时，（5.4.19）式中z的系数中至少有5个大于0，它们分别是x4，x6，x7，x8，x9的系数，因此为了使y取最小值，x4，x6，x7，x8，x9应尽可能取0，而根据前面的计算知道约束条件已经保证至少要选修6门课，所以x4，x6，x7，x8，x9中最多只能有3个同时取0，这与λ1=1，λ2=0的情况，即选修的课程数最少是一样的.

评注：用0-1变量表示选择策略是常用的方法，而对于“要选甲必选乙”这样的约束，可以用类似于（5.4.10）式x4≤x7来描述.有些选择问题，如从众多球员中选拔上场队员时，由于相互配合或相互制约的关系，还会遇到诸如“甲乙二人至多选一人”“甲乙二人至少选一人”“要选甲必不能选乙”等约束.

本节还讨论了多目标规划问题的处理办法，其基本思想是通过加权组合形成一个新的目标，从而化为单目标规划.优先考虑一个目标不过是这种办法的极端情况，而像前面同学乙那样，把一个目标作为约束条件（5.4.17），解另一个目标的规划模型，也是处理多目标规划的方法.