自来水输送与货机装运-数学建模方法

钢铁、煤炭、水电等生产、生活物资从若干供应点运送到一些需求点，怎样安排输送方案使运费最小，或者利润最大？各种类型的货物装箱，由于受体积、质量等的限制，如何相互搭配装载，使获利最高，或者装箱数量最少？本节将通过两个例子讨论用数学规划模型解决这类问题的方法.

一、自来水输送问题

某市有甲、乙、丙、丁四个居民区，自来水由A，B，C三个水库供应.四个区每天必须得到保证的基本生活用水量（单位：103 t）分别为30，70，10，10，但由于水源紧张，三个水库每天最多只能分别供应自来水50，60，50.由于地理位置的差别，自来水公司从各水库向各区送水所需付出的引水管理费不同（见表5.2.1，其中C水库与丁区之间没有输水管道），其他管理费用（单位：元/103 t）都是450.根据公司规定，各区用户按照统一标准900收费.此外，四个区都向公司申请了额外用水量，分别为每天50，70，20，40.该公司应如何分配供水量，才能获利最多？

表5.2.1　从水库向各区送水的引水管理费

为了增加供水量，自来水公司正在考虑进行水库改造，使三个水库每天的最大供水量都提高一倍，问那时供水方案应如何改变？公司利润可增加到多少[1]？

【问题分析】

分配供水量就是安排从三个水库向四个区送水的方案，目标是获利最多.而从题目给出的数据看，A，B，C三个水库的供水量160，不超过四个区的基本生活用水量与额外用水量之和300，因而总能全部卖出并获利.于是自来水公司每天的总收入是900×(50+60+50)=144000元，与送水方案无关.同样，公司每天的其他管理费用450×(50+60+50)=72000元，也与送水方案无关.所以，要使利润最大，只需使引水管理费最小即可.另外，送水方案自然要受三个水库的供应量和四个区的需求量的限制.

【模型建立】

很明显，决策变量为A，B，C三个水库(i=1，2，3)分别向甲、乙、丙、丁四个区(j=1，2，3，4)的供水量.设水库i向j区的日供水量为xij.由于C水库与丁区之间没有输水管道，即x34=0，因此只有11个决策变量.

由上分析，问题的目标可以从获利最多转化为引水管理费最少，于是有

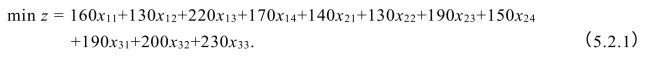
约束条件有两类：一类是水库的供应量限制，另一类是各区的需求量限制.

由于水总能卖出并获利，水库的供应量限制可以表示为：

考虑到各区的基本生活用水量与额外用水量，需求量限制可以表示为：

【模型求解】

（5.2.1）～（5.2.8）构成一个线性规划模型（当然加上xij的非负约束）.输入LINGO：

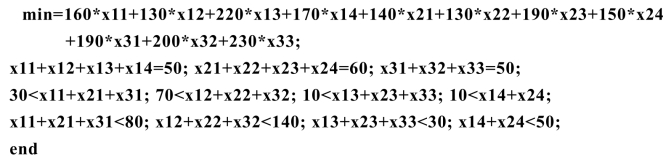
求解得到送水方案为（输出结果略）：A水库向乙区供水50，B水库向乙、丁区分别供水50、10，C水库向甲、丙分别供水40、10.引水管理费为24400元，利润为144000-72000-24400=47600元.

讨论：如果A，B，C三个水库每天的最大供水量都提高一倍，则公司总供水能力为320，大于总需求量300，水库供水不能全部卖出，因而不能像前面那样，将获利最多转化为引水管理费最少.此时我们首先需要计算A，B，C三个水库分别向甲、乙、丙、丁四个区供应每103 t水的净利润，即从收入900元中减去其他管理费450元，再减去表5.2.1中的引水管理费，得表5.2.2.

表5.2.2　从水库向各区送水的净利润

于是决策目标为

由于水库供水量不能全部卖出，所以上面约束（5.2.2）～（5.2.4）的右端增加一倍的同时，应将=改成≤，即

约束（5.2.5）～（5.2.8）不变.将（5.2.5）～（5.2.12）构成的线性规划模型输入LINGO求解得送水方案为（详细程序和输出结果略）：A水库向乙区供水100，B水库向甲、乙、丁区分别供水30、40、50，C水库向甲、丙区分别供水50、30，总利润为88700元.

其实，由于每个区的供水量都能完全满足，所以上面（5.2.5）～（5.2.8）每个式子左边的约束可以去掉，右边的≤可以改写成=.做这样的简化后得到的解没有任何变化.

评注：本题考虑的是将某种物质从若干供应点运往一些需求点，在供需量约束条件下使总费用最小或总利润最大.这类问题一般称为运输问题，是线性规划应用最广泛的领域之一.在标准的运输问题中，供需量通常是平衡的，即供应点的总供应量等于需求点的总需求量.本题中供需量不平衡，但这并不会引起本质的区别，同样可以方便地建立线性规划模型求解.

二、货机装运

某架货机有三个货舱：前仓、中仓、后仓.三个货舱所能装载的货物的最大质量和体积都有限制，如表5.2.3所示.并且为了保持飞机的平衡，三个货舱中实际装载货物的质量必须与其最大容许质量成比例.

表5.2.3　三个货舱装载货物的最大容许质量和体积(www.xing528.com)

现有四类货物供该货机本次飞行装运，其有关信息如表5.2.4所示，最后一列指装运后所获得的利润.

表5.2.4　四类装运货物的信息

应如何安排装运，才使该货机本次飞行获利最大？

【模型假设】

问题中没有对货物装运提出其他要求，我们可做如下假设：

（1）每种货物可以分割到任意小.

（2）每种货物可以在一个或多个货舱中任意分布.

（3）多种货物可以混装，并保证不留空隙.

（4）所给出的数据都是精确的，没有误差.

【模型建立】

决策变量：用xij表示第i种货物装入第j个货舱的质量（t），货舱j=1，2，3分别表示前仓、中仓、后仓.

已知参数：货舱j的质量限制WETj，体积限制VOLj；第i种货物的质量wi.单位质量的体积vi，利润pi.用行向量表示，即

WET=(10，16，8)，VOL=(6800，8700，5300)；w=(18，15，23，12)，v=(480，650，580，390)，p=(3100，3800，3500，2850).

目标是最大化总利润，即

约束条件包括以下四个方面（除对xij的非负约束外）：

（1）供装载的四种货物的总质量约束，即

（2）三个货舱的质量限制，即

（3）三个货舱的空间限制，即

（4）三个货舱装入质量的平衡约束，即

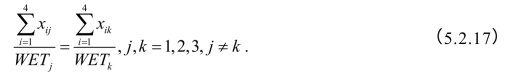
【模型求解】

将上述模型输入LINGO（注意这里通过集合定义变量，程序简洁、清晰，而且很容易推广）：

求解可以得到（以下只保留主要结果）：

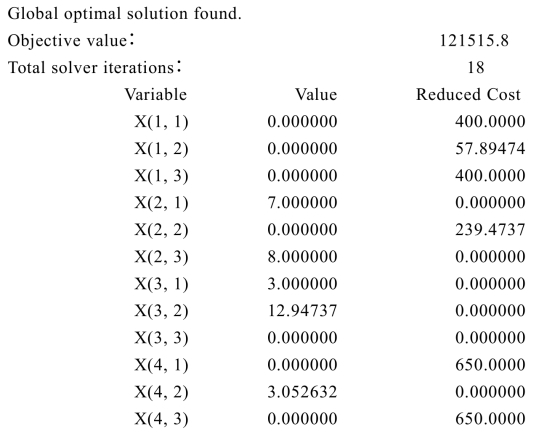
实际上，不妨将所得最优解四舍五入，结果为货物2装入前仓7 t、装入后仓8 t；货物3装入前仓3 t、装入中仓13 t；货物4装入中仓3 t.最大利润约121516元.（注意：这个问题的最优解并不唯一，但LINGO只能给出一个解）.

评注：初步看来，本例与运输问题类似，似乎可以把四种货物看成四个供应点，三个货舱看成三个需求点（或者反过来，把货舱看成供应点，货物看成需求点）.但是，这里对供需量的限制包括两个方面：质量限制和空间限制，且有装载平衡要求.因此，它只能看成运输问题的一种变形和扩展，这里学生需要体会模型的可移植性.