矩阵理论是线性代数中最重要的一个部分,矩阵是数学中极其重要并且应用广泛的工具.本节首先介绍矩阵及其相关的概念,然后介绍矩阵的相等、线性运算、矩阵乘法及相应的运算律.
一、矩阵概念
由![]() 个数aij构成的m行n列数表
个数aij构成的m行n列数表
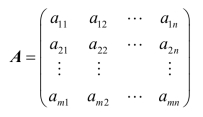
称为![]() 维(型)的矩阵(matrix),简称为
维(型)的矩阵(matrix),简称为![]() 矩阵.记为A=(aij )m×n,Am× n 或A=(aij ),其中aij为矩阵的第i行第j列元素,i=1,2,…,m为行标,j=1,2,…,n为列标.
矩阵.记为A=(aij )m×n,Am× n 或A=(aij ),其中aij为矩阵的第i行第j列元素,i=1,2,…,m为行标,j=1,2,…,n为列标.
注:矩阵一般用大写黑体字母A,B,…表示.
例1 试写出4 ×5矩阵A,其元素aij =2i -j.
解 由已知条件得
![]()
则

例2 试写出游戏“石头、剪刀、布”的二人零和对策中甲的得分矩阵,规定胜者得1分,败者得-1分,平手各得零分.
解 依题意
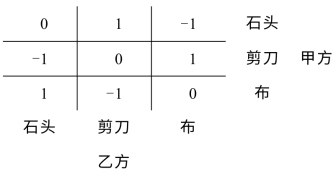
所以
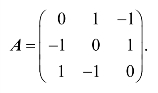
二、矩阵的线性运算(矩阵加法、数乘)
1.矩阵相等
设有两个m×n矩阵

若a ij=bi j (i=1,2,…,m; j=1,2,…,n),则称矩阵A和B相等,记作A=B.
注意:矩阵相等必须满足:行列对应相等且元素对应相等.
2.矩阵加法
设有两个m×n矩阵
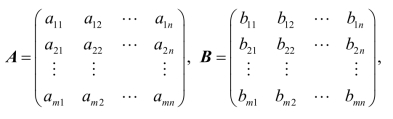
矩阵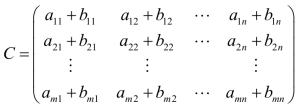 称为矩阵A与B的和,记作C =A +B=(ai j+bij )m×n .
称为矩阵A与B的和,记作C =A +B=(ai j+bij )m×n .
注意:只有同型的两个矩阵才能进行加法运算.
3.矩阵减法
设A=(aij )m×n ,负矩阵定义为:-A=(-aij )m×n =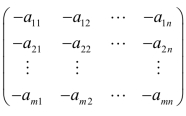 .
.
O=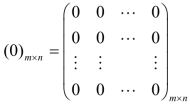 称为m ×n零 矩阵.
称为m ×n零 矩阵.
矩阵的减法定义为:
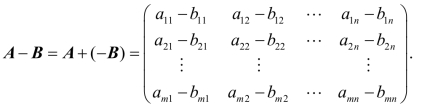
4.加法运算律
(1)A+B=B+A;
(2)(A+B)+C=A+(B+C);
(3)A+O=O+A=A;
(4)A-A=A+(-A)=O,
其中,A,B,C及零矩阵O是同型矩阵.
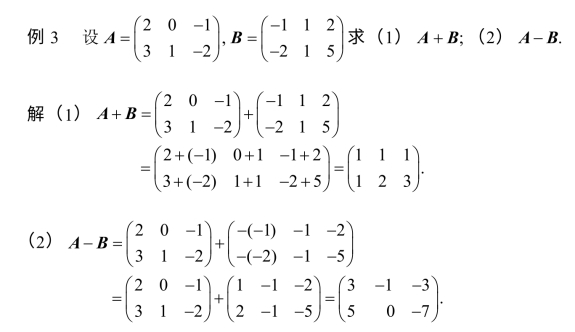
5.数乘矩阵
数k与矩阵A的乘积记作kA,规定为:
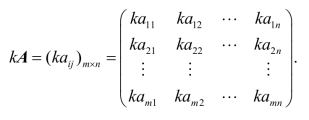
其运算规律如下:
(1)k(A+B)=kA+kB;(https://www.xing528.com)
(2)(k+h)A=kA+hA;
(3)k(h A)=(k h)A;
(4)1A=A,
其中A,B为![]() 矩阵;k,h为数.
矩阵;k,h为数.

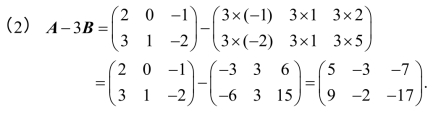
例5 如果矩阵X满足X-2A=B-X,其中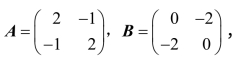 求X.
求X.
解 因为X-2A =B -X,所以![]() 则
则
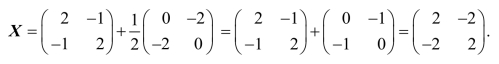
三、矩阵的转置
把矩阵A的行换成同顺序的列得到的新矩阵叫做A的转置矩阵,记作AT.
例如: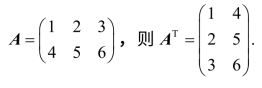
四、矩阵乘法
引例某服装商店一天的牛仔裤销售量如表3.5.1所示,且知每条W牌、L牌、CF牌、BO牌、BA牌牛仔裤的利润分别为15元、17.5元、20元、12.5元、20元.
表3.5.1 某店牛仔裤销量表

问题1:这一天内,最小号牛仔裤的销售利润总和是多少?
问题2:30号牛仔裤的利润总和是多少?
问题3:所有牛仔裤的销售利润总和是多少?
解 由已知得:利润矩阵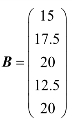 ,销量矩阵
,销量矩阵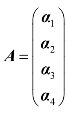 .
.

所以,所有牛仔裤的销售利润总和为120+387.5+257.5+97.5=862.5(元).
设矩阵A=(aij )m×s,B=(bij )s×n ,矩阵A与B的乘积是一个m×n矩阵C=(cij )m×n ,其中
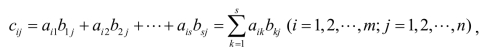
记作C=AB.
注:(1)只有当第一个矩阵(左矩阵)的列数等于第二个矩阵(右矩阵)的行数时,两个矩阵才能相乘.
(2)乘积矩阵AB=C的第i行第j列元素cij是A的第i行与B的第j列对应元素乘积之和.
(3)一个![]() 矩阵与一个
矩阵与一个![]() 矩阵的乘积是一个1阶矩阵,也就是一个数.
矩阵的乘积是一个1阶矩阵,也就是一个数.
例如: C=AB=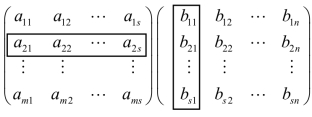 ,
,
即c21=a 21b 1 1+a 22 b21+…+a 2s bs1 .
例6 求矩阵A=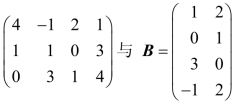 的乘积AB.
的乘积AB.

例7 求矩阵A=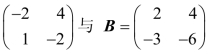 的乘积AB 与BA.
的乘积AB 与BA.
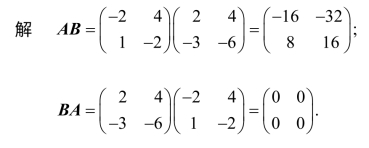
一般地:(1)矩阵的乘法不满足交换律,即AB BA;
(2)两个非零矩阵的乘积可能是零矩阵.即由AB=O不能推出A=O或B=O.
例8 设矩阵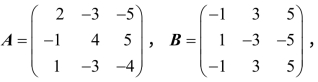 计算AO,AB.
计算AO,AB.
解 显然AO=O;
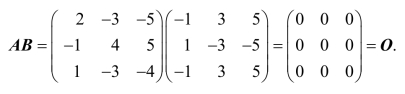
矩阵乘法不满足消去律,即由AB=AC不能推出B=C.
矩阵的乘法运算规律(假设运算都是可行的):
(1)(AB)C=A(BC);
(2)A(B+C)=AB+AC,(B+C)A=BA+CA;
(3)k(AB)=(kA)B=A(kB)(其中k为数).
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




