中学数学建模方法-平面向量核心知识

一、平面向量的五个基本概念

（1）零向量模的大小为0，方向是任意的，它与任意非零向量都共线，记为0或0→.

（2）长度等于1个单位长度的向量叫做单位向量，a的单位向量为.

（3）方向相同或相反的向量叫做共线向量（平行向量）．

（4）如果直线l的斜率为k，则a=(1，k)是直线l的一个方向向量．

（5）向量的投影：叫做向量b在向量a方向上的投影．

二、向量的两个定理

1.向量共线定理

（1）实数与向量的积：实数λ与向量a的积是一个向量，记作λa，它的长度与方向规定如下：

①.

②当λ＞0时，λa的方向与a的方向相同；

当λ＜0时，λa的方向与a的方向相反；

当λ=0时，λa=0，方向是任意的。

（2）两个向量共线定理：向量b与非零向量a共线有且只有一个实数λ，使得b=λa.

2.平面向量基本定理

如果e1 ,e2是一个平面内的两个不共线向量，那么对这一平面内的任一向量a，有且只有一对实数λ 1,λ2使得a=λ1e 1+λ2 e2，其中不共线的向量e1 ,e2叫做表示这一平面内所有向量的一组基底.

三、向量的充要条件及性质

1.向量的坐标

平面内向量的基底固定为x轴正方向、y轴正方向的单位向量,i j时，平面内的任一向量x y=+ai j.则向量(，)x y=a.

2.平面向量的两个充要条件

若两个非零向量a=(x1，y1)，b=(x2，y2)，则：

（1）a∥b a=λb x1y2-x2y1=0.

（2）a⊥b a·b=0 x1x2+y1y2=0.

3.平面向量的三个性质

（1）若a=(x，y)，则.

（2）若A(x1，y1)，B(x2，y2)，则.

（3）若a=(x1，y1)，b=(x2，y2)，θ为a与b的夹角，则

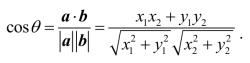
四、向量的应用

1.类型一　平面向量的概念及线性运算

例1　（1）设D，E分别是△ABC的边AB，BC上的点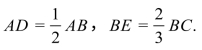，若(λ1，λ2为实数)，则λ1+λ2的值为________．

（2）△ABC的外接圆的圆心为O，半径为2，且，则向量在上的投影为（　　）.

答案　（1）；（2）A.

解　（1）如图3.4.1（a）所示，

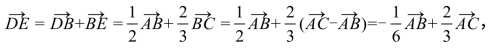
则.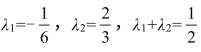

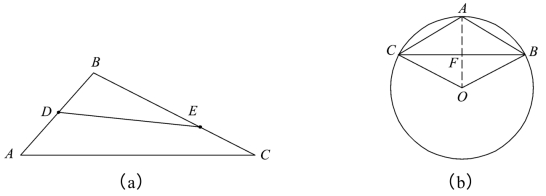
图3.4.1　例1的图

（2）如图3.4.1（b）所示，由=0，

得.

又O为△ABC外接圆的圆心，OB=OC，

所以四边形ABOC为菱形，AO⊥BC.

由=2，(www.xing528.com)

知△AOC为等边三角形．

故上的投影为.

反思：（1）在一般向量的线性运算中，只要把其中的向量当作字母，其运算就类似于代数中合并同类项的运算；有的问题采用坐标解决更简单．

（2）运用向量加减法解决几何问题时，要善于发现或构造三角形或平行四边形，使用三角形法则时要特别注意“首尾相接”.运用平行四边形法则时两个向量的起点必须重合．

2.类型二　平面向量的数量积

例2　（1）如图3.4.2所示，在矩形ABCD中，，BC=2，点E为BC的中点，点F在边CD上，若，则的值是________．

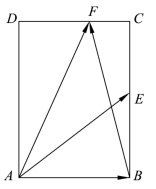
图3.4.2　例2的图

（2）若a，b，c均为单位向量，且a·b=0，(a-c)·(b-c)≤0，则|a+b-c|的最大值为（　　）.

答案　（1）；（2）B.

解　（1）方法1　坐标法．

以A为坐标原点，AB，AD所在直线为x轴、y轴建立平面直角坐标系，

则A(0，0)，B(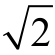，0)，E(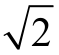，1)，F(x，2)．

故.

所以.

又，所以x=1.

所以．

所以.

方法2　用表示是关键．

设

?，则

?

又因为，所以.所以.

所以.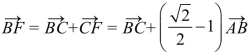

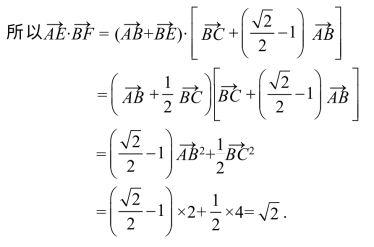
（2）方法1　由题意知a2=b2=c2=1.

又因为a·b=0，

(a-c)·(b-c)=a·b-a·c-b·c+c2≤0，

所以a·c+b·c≥c2=1.

所以|a+b-c|2=a2+b2+c2+2a·b-2a·c-2b·c=3-2(a·c+b·c)≤1.

所以|a+b-c|≤1.

方法2　设a=(1，0)，b=(0，1)，c=(x，y)，

则x2+y2=1，a-c=(1-x，-y)，b-c=(-x，1-y).

则(a-c)·(b-c)=(1-x)(-x)+(-y)(1-y)

=x2+y2-x-y=1-x-y≤0，

即x+y≥1.

又a+b-c=(1-x,1-y)，

所以|a+b-c|=.

反思：（1）涉及数量积和模的计算问题，通常有两种求解思路：

①直接利用数量积的定义；

②建立坐标系，通过坐标运算求解．

（2）在利用数量积的定义计算时，要善于将相关向量分解为图形中模和夹角已知的向量进行计算．

求平面向量的模时，常把模的平方转化为向量的平方．