一、重要知识点
1.数列
（1）定义：按照一定次序排列的一列数称为数列，数列中的每一个数叫做这个数列的项，如：数列1，3，5，7，….
数列是一种特殊的函数（定义域为正整数集的函数）.
（2）通项公式：如果数列｛an ｝的第n项an与项数n之间的关系可以用一个式子来表示，则这个公式称为通项公式，其中n∈N+或n∈N*（可省略）.
（3）前n项和：S n =a1 +a 2+a 3+a4+…+an ，n∈N+.
（4）an与Sn的关系：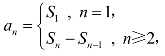
（常用来求通项公式）.
2.等差数列
（1）定义：如果一个数列从第2项起，每一项与它前一项的差等于同一常数，则该数列叫做等差数列，这个常数叫做公差，常用字母d表示，即
a n-an-1=d (n≥2且n∈N*)或an+1-a n =d (n∈N+).
（2）通项公式：a n =a1+(n-1)d.（注意变式）
（3）等差中项：若x，A，y成等差数列，则称A为x与y的等差中项，即
.
（4）重要性质：若m +n =p +q ，则a m+a n=a p+aq.
（5）前n项和：
3.等比数列
（1）定义：如果一个数列从第2项起，每一项与它前一项的比等于同一个非零常数，则该数列叫做等比数列，这个常数叫做公比，常用字母q表示，即
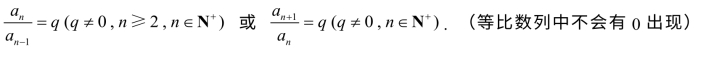
（2）通项公式：a n=a1 qn-1.（注意变式）
（3）等比中项：若x，G，y成等比数列，则称G为x与y的等比中项，即G 2=x y.
（4）重要性质：若m +n =p +q ，则a m a n=a p aq.
（5）前n项和：
.
4.等差数列和等比数列的对比（见表3.1.1）
表3.1.1 等差数列和等比数列对比表
二、数列应用的模型
（1）等差模型：如果增加（或减少）的量是一个固定量，则该模型是等差模型，增加（或减少）的量就是公差．
（2）等比模型：如果后一个量与前一个量的比是一个固定的数，则该模型是等比模型，这个固定的数就是公比．
（3）混合模型：在一个问题中同时涉及等差数列和等比数列的模型．
（4）生长模型：如果某一个量，每一期以一个固定的百分数增加（或减少），同时又以一个固定的具体量增加（或减少）时，我们称该模型为生长模型．如分期付款问题、树木的生长与砍伐问题等．
（5）递推模型：如果容易找到该数列任意一项an与它的前一项an-1（或前n项）间的递推关系式，我们可以用递推数列的知识来解决此问题.
例1（2012·湖南） 某公司一下属企业从事某种高科技产品的生产．该企业第一年年初有资金2000万元，将其投入生产，到当年年底资金增长了50%，预计以后每年资金年增长率与第一年的相同．公司要求企业从第一年开始，每年年底上缴资金d万元，并将剩余资金全部投入下一年生产．设第n年年底企业上缴资金后的剩余资金为an万元．
（1）用d表示a1，a2，并写出an+1与an的关系式；(www.xing528.com)
（2）若公司希望经过m(m≥3)年使企业的剩余资金为4000万元，试确定企业每年上缴资金d的值（用m表示）．
分析：（1）由第n年和第(n+1)年的资金变化情况得出an与an+1的递推关系；
（2）由an+1与an之间的关系可求出通项公式，问题便可求解．
解 （1）由题意得
（2）由（1）得
整理得
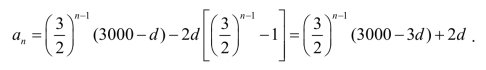
由题意知am=4000，即
解得
故该企业每年上缴资金d的值为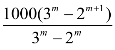
时，经过m(m≥3)年企业的剩余资金为4000万元．
例2 某产品在不做广告宣传且每千克获利a元的前提下，可卖出b千克．若做广告宣传，广告费为n(n∈N*)千元时比广告费为(n-1)千元时多卖出
千克．
（1）当广告费分别为1千元和2千元时，用b表示销售量S；
（2）试写出销售量S与n的函数关系式；
（3）当a=50，b=200时，要使厂家获利最大，销售量S和广告费n分别应为多少？
解 （1）当广告费为1千元时，销售量
；
当广告费为2千元时，销售量
.
（2）设Sn(n∈N)表示广告费为n千元时的销售量，由题意得：
以上n个等式相加得
即
（3）当a=50，b=200时，设获利为Tn，则有
设
，则
当n≤2时，bn+1-bn＞0；当n≥3时，bn+1-bn＜0.所以当n=3时，bn取得最大值，即Tn取得最大值，此时Sn=375，即该厂家获利最大时，销售量和广告费分别为375千克和3千元．
反思：用数列知识解相关的实际问题，关键是合理建立数学模型——数列模型，弄清所构造的数列的首项是什么，项数是多少，然后转化为解数列问题．求解时，要明确目标，即搞清是求和，还是求通项，还是解递推关系问题，所求结论对应的是解方程问题，还是解不等式问题，还是最值问题，然后进行合理推算，得出实际问题的结果．
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
