中学数学建模方法简介

一、函数模型

函数反映了事物间的广泛联系，揭示了现实世界众多的数量关系及运动规律，现实生活中，诸如获利最大、用料最省、投资最佳、成本最小、方案最优化等问题，常可建立函数模型来求解.

例1（消防损失最小问题）　森林失火了，火势正以每分钟100平方米的速度顺风蔓延.消防站接到警报后立即派消防队员前去，在失火后5分钟到达现场救火.已知消防队员在现场每人每分钟可灭火50平方米，所消耗的灭火材料、劳务津贴等费用为每人每分钟125元，另附加每次救火所损耗的车辆、器械和装备等费用平均每人100元，而每烧毁一平方米森林的损失费为60元，问应该派多少名消防队员前去救火，才能使得总损失最小？

分析：总损失费=森林损失费+灭火材料费+车辆器械费，

其中，森林损失费=每平方米损失费×面积

=每平方米损失费×每分钟蔓延面积×时间

=60 ×100×(5+t )；

灭火材料费=每单位时间人均费用×人数×时间=125×x×t；

车辆器械费=人均车辆器械费×人数=100×x；

灭火面积=新增过火面积+原有过火面积，即50×x ×t=100t +500.

解　设需要x名消防员，t分钟救火时间，由题意可知

50×x×t=100t+500，

即

由条件列出森林损失费与救火费用的总损失费用的目标函数为

y =60 ×100×(5+t)+125xt+100x.

代入，得

即当x=27时，总损失最小，最小损失为36450元.

例2（淋雨问题）　如图2.2.1所示，长方体物体E在雨中沿面P（面积为S）的垂直方向作匀速移动，速度为v(v＞0)，雨速沿E移动方向的分速度为c （c∈R）.E移动时单位时间内的淋雨量包括两部分：（1）P或P的平行面（只有一个面淋雨）的淋雨量，假设其值与成正比，比例系数为；（2）其他面的淋雨量之和，其值为. 记y为E移动过程中的总淋雨量，当移动距离d=100，面积S=.

（1）写出y的表达式；

（2）设0＜v≤10，0＜c≤5，试根据c的不同取值范围，确定移动速度v，使总淋雨量y最少？

图2.2.1　淋雨示意图

解　（1）由题意知，E移动时单位时间内的淋雨量为，故

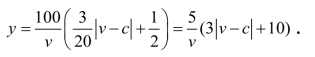
（2）由（1）知，当0 v c≤≤时，

当c ＜v≤10时，

故

①当时，y是关于v的减函数．故当v=10时，．

②当时，在(0，c]上，y是关于v的减函数；在(，10c]上，y是关于v的增函数．故当v=c时，．

例3（轮滑跑道问题）　轮滑是穿着带滚轮的特制鞋在坚硬的场地上滑行的运动．如图2.2.2所示，助跑道ABC是一段抛物线，某轮滑运动员通过助跑道获取速度后飞离跑道然后落到离地面高为1米的平台上E处，飞行的轨迹是一段抛物线CDE（抛物线CDE与抛物线ABC在同一平面内），D为这段抛物线的最高点．现在在运动员的滑行轨迹所在平面上建立如图所示的直角坐标系，x轴在地面上，助跑道一端点A(0，4)，另一端点C(3，1)，点B(2，0)，单位：米．

（1）求助跑道所在的抛物线方程；

（2）若助跑道所在抛物线与飞行轨迹所在抛物线在点C处有相同的切线，为使运动员安全和空中姿态优美，要求运动员的飞行距离在4米与6米之间（包括4米和6米），试求运动员在飞行过程中距离平台最大高度的取值范围？（注：飞行距离指点C与点E的水平距离，即这两点横坐标差的绝对值．）

图2.2.2　轮滑跑道示意图

解　（1）设助跑道所在的抛物线方程为f (x )=a0 x 2+b0 x +c0，依题意得

解得a0=1，b0=-4，c0=4.所以助跑道所在的抛物线方程为

f (x )=x2-4 x+4.

（2）设飞行轨迹所在抛物线为g (x )=ax 2+bx +c (a＜0)，依题意得

得

解得所以

令g (x)=1，得

因为a＜0，所以.

当时，g (x)有最大值为，则运动员的飞行距离

飞行过程中距离平台最大高度

依题意，得

即飞行过程中距离平台最大高度的取值范围为2米与3米之间．

二、方程（组）模型

现实生活中广泛存在着数量之间的相等关系.方程（组）模型是研究现实世界数量关系的最基本的数学模型，它可以帮助人们从数量关系的角度更正确、清晰地认识、描述和把握现实世界.诸如纳税问题、分期付款问题、打折销售问题、增长率问题、储蓄利息问题、工程问题、行程问题、浓度配比问题等，常可以抽象成“方程（组）”模型，通过列方程（组）加以解决.

例4（耕地规划问题）　某地现有耕地1万公顷，规划10年后，粮食单产比现在增加22%，人均粮食占有量比现在提高10%，如果人口年增加率为1%，那么耕地平均每年至多只能减少多少公顷？

解　建立数学模型：找出题中所涉及的对象，并用符号表示如下：

现有土地数量M1，十年后土地数量M2；

现有单产量N1，十年后单产量N2；

现有人口数P1，十年后人口数P2；

现人均占有量A1，十年后人均占有量A2，这些量之间具有如下关系：

由此可得

若设平均每年耕地减少量为x公顷，则有如下关系：

M2=M1-10x.

对（2.2.1）式化简整理，并代入M1=104，得

(www.xing528.com)

关于x的上述方程即可作为原题的数学模型，注意到x增大时，方程右端的值单调减少，所以根据这一模型的解x≈4来给出原题的答案时，应是x至多为4，即x≤4，也即平均每年减少至多4公顷.

三、不等式（组）模型

现实生活中同样也广泛存在着数量之间的不等关系.诸如统筹安排、市场营销、生产决策、核定价格范围等问题，可以通过给出的一些数据进行分析，将实际问题转化成相应的不等式问题，利用不等式的有关性质加以解决.

例5（服装的降价幅度问题）　某种服装原来以高于成本价的40%出售，根据市场调查，原价每降低1个百分点，月销售件数将增加10个百分点.为使月毛利润（月毛利润=月销售总额-月成本总额）比原来增加幅度不小于30%，问降价至多多少个百分点？

分析　从整体上看，这是一个服装销售过程中计算毛利润问题，涉及服装的成本价、原价、月销售件数、月销售总额、月成本总额、降价等概念，但从局部来看，关键是要处理好上述各量之间的关系，在选准基准量后，应分析降价前后的服装销售毛利润.

解　设原价为a，销售件数为b，价格降低的百分比为x，列表2.2.1分析如下：

表2.2.1　成本、售价、销量、利润

数量关系式为

公式化简得

-70x2+13x-0.6≥0.

解得x≤0.1.

答：降价至多10个百分点.

四、三角函数模型

三角函数在测算距离、高度、角度等几何相关实际问题中有着广泛的应用，且有大量的公式和优良的性质，在实际中应用也非常灵活.

例6（港口停泊时间问题）　通常情况下，船在涨潮时驶进航道，靠近船坞，落潮时离开.某港口水深y与时间t的函数记作y=(f)t，表2.2.2是该港口在某季节每时水深的数据：

表2.2.2　某港某季节各时段水深数据

经长期观察，y=f(t)的曲线可以近似看作函数的图像.问：一般情况下，船舶航行时船底到海底的距离在5米或5米以上是安全的，某船吃水深度为6.5米，如果该船想在同一天进出港，问至多能停留多久？

解　根据数据得

船出港时水深不小于5+6.5=11.5米，即

得

同一天内取1k=或0，得15t≤≤，1317.t≤≤所以最早凌晨1点进港，最迟下午17点出港.

例7（飞轮传动问题）　如图2.2.3所示，两个圆形飞轮通过皮带传动，大飞轮1O的半径为2r(r为常数)，小飞轮2O的半径为r，1 2 4O Or=.在大飞轮的边缘上有两点A，B，满足，在小飞轮的边缘上有一点C．设大飞轮逆时针旋转一圈，传动开始时，点B，C在水平直线1 2O O上．

（1）求点A到达最高点时A，C间的距离；

（2）求点B，C在传动过程中高度差的最大值.

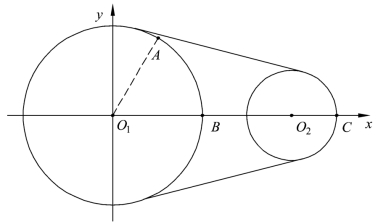
图2.2.3　飞轮传动示意图

解　（1）以1O为坐标系的原点，1 2O O所在直线为x轴，如图2.2.3所示，建立直角坐标系．当点A到达最高点时，点A绕O1转过，则点C绕O2转过．此时，A(0，2r)，C．所以

（2）由题意，设大飞轮转过的角度为θ，则小飞轮转过的角度为2θ，其中θ∈[0，2π]．此时，B(2r cosθ，2r sinθ)，C(4r+r cos2θ，r sin 2θ)．

记点B，C高度差为d，则

d=|2 rsinθ-rsin 2θ|．

即

d=2r|sinθ-sin θcosθ|．

设f (θ)=sinθ-sin θcosθ ，θ∈[0，2π]，则

f ′(θ)=(1 -cosθ)(2cosθ+1)．

令f ′(θ)=(1 -cosθ)(2cosθ+1)=0，得cosθ=或1．则θ=，0或2π．

列表2.2.3如下：

表2.2.3

所以当时，f(θ)取得极大值为；当时，f(θ)取得极小值为．所以，点B，C在传动中高度差的最大值．

五、数列模型

现实世界的经济活动中，诸如增长率、降低率、复利、分期付款等与年份有关的实际问题常常归结为数列问题，可通过建立数列模型来解决.

例8（购房付款方式问题）　某房地产开发公司因有大量住房闲置，为盘活资金，促进住房销售，提出了两种优惠售房方案：第一种方案是分期付款，2000年元月要求购房者先付12万元，然后从第二年起每年元月付款2万元，连续付5年（假设这5年中银行存款的年利率为2%）；第二种方案是2000年元月一次性付款21.2万元.如果购房者都从银行取款购房，试问：他们采用哪一种方案付款合算，请加以说明.（结果精确到小数点后两位，计算时，可以选用如下数据：1.024≈1.08，1.025≈1.10，1.026≈1.13）.

解　终值比较法，选择比较的时点是2005年元月.

分期付款模型：

经分析得

S分=12(1+2%)5+2(1+2%)4+…+2(1+2%)+2≈23.2万元；

S合=21.2×1.025≈23.32万元，

可见第一种方案比较合算.

例9　某啤酒厂为适应市场需要，2011年起引进葡萄酒生产线，同时生产啤酒和葡萄酒，2011年啤酒生产量为16000吨，葡萄酒生产量1000吨.该厂计划从2012年起每年啤酒的生产量比上一年减少50%，葡萄酒生产量比上一年增加100%，试问：

（1）哪一年啤酒与葡萄酒的年生产量之和最低？

（2）从2011年起（包括2011年），经过多少年葡萄酒的生产总量不低于该厂啤酒与葡萄酒生产总量之和的？（生产总量是指各年年产量之和）

解　设从2011年起，该厂第n年啤酒和葡萄酒年生产量分别为an吨和bn吨，经过n年后啤酒和葡萄酒各年生产量的总量分别为An吨和Bn吨．

（1）设第n年啤酒和葡萄酒生产的年生产量为Dn吨，根据题意，得

则

故2013年啤酒和葡萄酒生产的年生产量之和最低，为8000吨．

（2）依题意，，得Bn≥2An .因为

所以

因为2n -1 ＞0，所以2n≥64 =26，故n≥6．因此，从第6年起，葡萄酒各年生产的总量不低于啤酒各年生产总量与葡萄酒各年生产总量之和的．

中学里的应用题都可转化为我们所熟悉的代数式、方程、不等式、函数及几何图形、几何关系等数学模型来解决.鉴于问题的多样性、灵活性，为了构建数学模型，应要求学生对有关数学知识充分理解，且要具备敏锐的观察力、良好的想象力、较强的抽象思维能力和创新意识等，而且还应要求学生具备较强的知识应用能力和实践能力.