错误系统：建立错误函数的研究

对于一个具体的论域和错误规则，选择合适的错误函数是非常重要的。一般要根据实际的需要选择。如果只是用来表示论域上对象的对错，那么可以选择经典错误函数，0为对，1为错；如果还要表示对象的错误程度大小，选择错误函数时，就要考虑对于论域的完备性以及与规则的实际相符性，以选择合适的错误函数。下面通过例子来说明。

例：假设论域：全体整数，规则G：0为正确的数。求该论域在该规则下的错误函数。

只表示对象的对错时，错误函数可以为

这样的函数为经典错误函数。

对于例子中同样的论域和规则，若要表示对象错误程度的大小，错误函数的选择总体上要符合以下两个条件：

(1)首先要考虑论域的完备性，例如选择函数因为该函数的定义域x 中并没有0，故不可以作为该论域在该规则下的错误函数。

(2)此外，还要考虑建立的错误函数与规则实际的相符性，即错误函数的错误值要与实际中的错误程度大小相同。

例如，函数或者f(x，G)＝x 2 都可以作为非负错误函数的表达式，但若错误函数值与自变量x 之间是线性关系而非非线性关系，选择函数f(x，G)＝|x|为错误函数的表达式。

对一个具体的子系统建立模糊错误函数进行分析，而对于模糊错误函数的选取也必须符合以上两个条件，且可以根据模糊函数常见的几种分布来选择。

(1)矩形分布或半矩形分布(图6-1)。

图6-1　矩形分布或半矩形分布

(a)偏小型半矩形分布；(b)偏大型半矩形分布；(c)中间型矩形分布

①偏小型[图6-1(a)]。

②偏大型[图6-1(b)]。

③中间型[图6-1(c)]。

(2)半梯形分布与梯形分布(图6-2)。

图6-2　半梯形分布和梯形分布

(a)右半梯形分布；(b)左半梯形分布；(c)梯形分布

①偏小型[图6-2(a)]。

②偏大型[图6-2(b)]。

③中间型[图6-2(c)]。

(3)半抛物型与抛物型分布(图6-3)。

图6-3　抛物型分布

(a)右半抛物型分布；(b)左半抛物型分布；(c)抛物型分布

①偏小型[图6-3(a)]。

②偏大型[图6-3(b)]。

③中间型[图6-3(c)]。

(4)指数型分布(图6-4)。

图6-4　指数型分布(www.xing528.com)

(a)偏小型指数分布；(b)偏大型指数分布；(c)中间型指数分布

①偏小型[图6-4(a)]。

②偏大型[图6-4(b)]。

③中间型[图6-4(c)]。

矩形分布是以某个值为分界点来判别对象的对错，可用于在某些商品生产过程中对一些物质含量指标的判别等问题。例如对于偏小型矩形分布，当商品某物质含量不大于指标含量时即错误的。梯形分布是指在某个区间上的错误值是线性的；抛物型分布是指在某个区间上的错误值是抛物型的；指数型分布是指在某个区间上的错误值是指数型分布的。

由于在判别规则中可能蕴含各种类型的指标，因此，在对象集U 中的元素u一定的前提下，错误函数可根据不同的指标类型选择不同的形式。

1.判别规则蕴含效益型指标

设判别规则就对象系统的某个状态si给出了效益型的指标，即要求si≥a，且si越小于a，错误值越大，那么根据这类指标特点，错误函数可以相应地选择模糊错误函数、具有临界点的错误函数或者非负错误函数等。

对于si∈(-∞，＋∞)，当∀si≥a≥0时，若其错误值都是零，那么可以选择模糊错误函数或非负错误函数。例如：

或者

而对于si∈(-∞，＋∞)，当∀si≥a≥0时，若其错误值出现负值，并随着si的增大错误值减小，那么就可以选择具有临界点的错误函数。例如：

2.判别规则蕴含成本型指标

设判别规则就对象系统的某个状态si给出了效益型的指标，即要求si≤a，且si越大于a，错误值越大，那么根据这类指标特点，错误函数也可以同判别规则蕴含效益型指标一样，相应地选择模糊错误函数、具有临界点的错误函数或者非负错误函数等。

3.判别规则蕴含固定型指标

设判别规则就对象系统的某个状态si给出了固定型的指标，即要求si＝a，且si越偏离a，错误值越大，那么根据这类指标特点，错误函数可以相应地选择模糊错误函数或者非负错误函数。如对于si∈(-∞，＋∞)，可选择模糊错误函数：

当然也可选择非负错误函数：

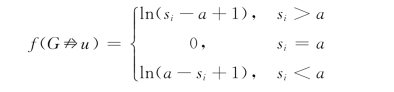
4.判别规则蕴含区间型指标

设判别规则就对象系统的某个状态si给出了区间型的指标，即要求si∈[a，b] ，且si越偏离区间[a，b]，错误值越大，那么根据这类指标特点，错误函数可以相应地选择模糊错误函数或者非负错误函数。如对于si∈(-∞，＋∞)，可选择如下形式的错误函数：

或者

5.判别规则蕴含接近型指标

设判别规则就对象系统的某个状态si给出了接近型的指标，即要求si≠a，且si越接近a，错误值越大，那么根据这类指标特点，错误函数可以相应地选择模糊错误函数或者非负错误函数。如对于si∈(-∞，＋∞)，可选择如下形式的错误函数：

或者

其中，α是正常数，β≥1。

6.判别规则蕴含接近区间型指标

设判别规则就对象系统的某个状态si给出了接近型的指标，即要求si∉[a，b] ，且si越接近区间[a，b]，错误值越大，那么根据这类指标特点，错误函数可以相应地选择模糊错误函数或者非负错误函数。如对于si∈(-∞，＋∞)，可选择如下形式的错误函数：

7.判别规则蕴含不可量化的定性指标

由于可量化的定性指标可以转化为前6种情况加以处理，所以对于定性指标只考虑不可量化的。如果判别规则蕴含不可量化的指标，那么错误函数的形式就可使用经典错误函数。例如：

在上述内容中，根据判别规则中可能蕴含的各类指标，给出了一些错误函数的具体形式。但它们仅是为了说明判别规则中所蕴含的各类指标对错误函数的影响而列举的一些简单形式。在实际应用中，错误函数的形式远不只这些，而且错误函数的具体形式还与实际需要密切相关。因此，错误函数的建立和具体形式的选择要根据具体问题具体分析，既要考虑判别规则，又要考虑客观实际的需要。一个总的原则就是所建立的错误函数要能够如实地反映判别对象对判别规则的违反程度。

在实际应用中可以根据讨论对象的特点加以选择，也可以通过统计资料作出大致曲线，将其与上述分布比较，选择最接近的一个，再根据实验确定较符合实际的参数。当然有些错误函数是由几种分布的并、交、余运算求得的。