错误系统元素关系分析:方法研究

在对象系统中，一般情况下，若其中一个要素变化，则会引起另一个要素也发生变化。例如，对象系统中的某个条件变化，则在一般情况下必然会引起该对象系统某些结论变化。同时，若对象系统的一个要素改变，则必然需要别的元素作相应的改变。例如，固有功能变换，一般情况结论也会随之改变。其变换影响如图3-1所示。

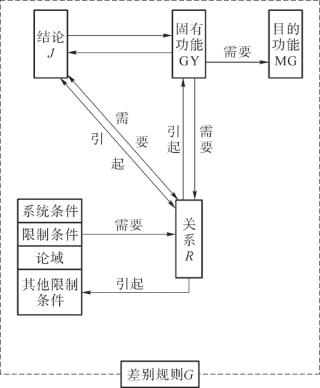
图3-1　变换影响

在探究一个系统时，知道这个系统是由一系列相互关联的元素组成的，这些元素有各自特有的状态，但这些状态经常会随着相关元素状态的变动而变化。因此，在一个出错的系统中，这个错误表现出来的是整个系统的错误，但知道该系统必定是由一个或多个元素的错误造成的。如何找到这些因素，从而消除系统错误，优化系统功能，是需要研究的内容。

定义3.2.6　有一个错误系统X，其中共有n个元素，如果对元素si，有实数ti与之对应，而且这个实数的值仅与元素si变化的最终结果有关，与其变化过程无关，则称ti是s i的状态值，其中i∈{1，2，…，n}。如果元素si的状态t i变化引起本系统中另一个元素s j的变化，则称si为s j的制约元素，sj为s i的被制约元素。如果元素sk的状态t k的变化能由本系统外的环境的变化所引起，则sk被称为系统的关卡元素。

定义3.2.7　如果有一个错误系统有关卡元素，则称这个系统为可调错误系统。

在实际中，真正有研究意义的错误系统，是可调的错误系统，因为只有错误系统可调，管理者才能按自己的意图去调整它的状态，使其转化为正确系统。

定义3.2.8　对于元素si，sj的当前状态值来说，如果si的状态值t i的变化量Δti会引起s j的状态值的变化量Δt j，而且Δt j是Δti的某种函数f(Δti)，则函数Δt j＝f(Δti)称为在当前状态下元素si对元素s j的制约函数，简称制约函数。

每一个被制约的元素可以有多个制约元素，所以，可以有多个制约元素状态变化引起被制约元素状态的变化。这样从制约元素的角度看，被制约的元素的状态值的变化实际上是它的所有制约元素的状态值变化量的函数。因此，一般来说，被制约元素的状态值的变化是各个制约元素的状态值变化量的多元函数。

为此设sb为被制约元素，它共有r个制约元素sb1，sb2，…，sbr，被制约元素的状态值是它的各个制约元素状态值的多元函数，即tb＝f(tb1，tb2，…，tbr)。

为了简便，考察制约函数是线性函数时的情况。

如果对于某个被制约元素sb来说，它的r个制约元素s b1，sb2，…，sbr对于它的制约函数都是线性齐次的，即对于被制约元素sb来说，如果它的各个制约函数为Δtb＝cbiΔtbi这种形式，则按照偏导数的意义，式中的常数cbi的数学意义应当是

所以，被制约元素sb与制约元素s bi之间的状态函数的线性形式为

如果在状态制约系统中的各个制约函数均为线性制约函数，那么该系统的状态调整优化就会较为方便。具体的分析方法如下：

为了弄清楚制约元素和被制约元素的关系，就要在复杂的系统中，通过对系统要素的分类寻找制约元素。

系统论认为，凡系统必有结构，系统结构决定系统的功能；破坏了系统的结构，也就破坏了系统的总体功能。这说明了系统的整体性与重要性特征。在一个错误系统中，结构可以抽象为：系统结构＝{所论系统的单元全体，单元间的联系或关系}。

显然，系统的结构因为一个元素的状态之间的相互作用关系变得非常复杂，为了使各阶子系统的关系明确无误地表达出来，可以建立如下矩阵，其方法如下。

1.求出邻接矩阵A(www.xing528.com)

2.建立可达矩阵

通过缩减可达矩阵，得到骨干矩阵。

3.调整元素状态的效率向量与效率函数向量

在状态制约系统中，各个元素的状态都是可以人为改变的。但是，这种改变一般要花费成本，这就是调整成本。调整成本一般不是常数，不同元素的调整成本往往不同，同一个元素在不同的当前状态时，调整成本也不同。此外，即使在同一个元素当前的同样状态下，调整方向是提高还是降低当前状态值，所消耗的成本也常常是不同的。

对于元素si来说，设它的状态调整成本中共有m 个类型的成本，如果将其当前状态值调整一个单位，所消耗的各方面的成本值所组成的向量为该元素的当前趋高效率向量，记为b＋i ＝(bi1，bi2，…，bim)，反之，如果将该元素的当前状态值降低一个单位，所消耗的各方面的成本值所组成的向量为该元素的当前趋低效率向量，记为p-i ＝(p i1，p i2，…，p im)。

需要的注意的是，效率向量中的各个分量可以是正数，也可以是负数，正数表示消耗的成本，而负数则表示在相应的方向上改变该元素的当前状态值时，不但不会消耗成本，反而在相应的分量上会释放一定的资源。比如，如果对学校系统中的“试验室规模”这个元素的当前状态值进行趋低调整，则会释放出一定的场地、设备等原来所占用的成本。

还要注意的是，相同元素的相同的成本分量的趋大值与趋小值一般并不关于原点对称，即bij≠-p ij，反而有时二者都是正的。这是因为，有些成本是单纯的、消耗性的，而不是可回收的。比如，对于“人工”这样的成本分量，为了提高元素ei的当前状态值而花费了一定的“人工”，如果后来又降低该元素的当前状态值，则不但不会释放出以前所消耗的“人工”，反而还要重新用掉许多“人工”。

对于某个元素来说，它的趋高效率向量和趋低效率向量的值都是针对当前状态值而言的。显然，随着不断地对其状态进行调整，其当前状态值也在不断地发生变化，其趋高效率向量或者趋低效率向量也会不断地发生变化，效率向量是受相应元素的状态值制约的，所以，效率向量可以看作元素的状态值的函数。

函数向量b＋i ＝[bi1(ti)，bi2(ti)，…，bim(ti)]称为元素si的趋高效率函数向量，函数向量p-i ＝[p i1(ti)，p i2(ti)，…，p im(ti)]称为元素si的趋低效率函数向量。二者都可称为元素si的效率函数向量。比较简单的效率函数向量是线性的，这时，对状态调整的优化计算会简单很多。

显然，对于状态制约系统的调整，只能通过调整入口元素的状态来实现，即通过对入口元素的状态的调整，先引起入口元素的状态变化，再引起以这些入口元素为制约元素的被制约元素的状态变化。所以，每当调整各个入口元素时，所引起状态变化的元素并不仅是入口元素本身，而是包括了入口元素和与入口元素相对应的各个被制约元素，同时还包括了被制约元素所制约的元素，即各个层次的间接的被制约元素。

状态制约系统中的入口元素sk的当前状态值提高一个单位，引起的该系统的各个元素的状态的变化幅度所组成的向量称为sk的趋高调整能力向量，记为c＋k ＝(Δt k1，Δt k2，…，Δt kn)，式中，n 为系统中的元素的总数目，Δt ki为在入口元素s k的状态值t k变化一个单位时，被制约元素(包括直接的被制约元素和间接的被制约元素)si的当前状态t i的变化量。如果sk的当前状态值降低一个单位，引起该系统的各个元素的状态值的变化幅度所组成的向量称为sk的趋低调整能力向量，记为c-k ＝(Δt k1，Δt k2，…，Δt kn)。在调整目标明确的情况下，对入口元素ek的调整方向是趋高还是趋低也是明确的，这时，为了简洁，不再区分趋高和趋低调整能力向量，而是统称为sk的调整能力向量，记为c k＝(Δt k1，Δt k2，…，Δt kn)。显然，各个入口元素的调整能力向量反映的是它们对系统状态的影响能力的大小。

一般来说，元素的状态变化要消耗一定的成本，而成本又是分为许多项目的，所以，元素变化所消耗的成本是一个向量。这样，对于一个入口元素的调整能力向量来说，它所表示的各个元素的状态值的变化量，也就对应着各个元素的状态在相应的变化量时所消耗的成本向量，同时，这些成本向量都是由入口元素的状态值变化一个单位引起的。这样，为了准确比较各个入口元素的当前状态值在变化一个单位时所需要消耗的总成本，要设法把这些由某个入口元素的状态变化所引起的各个元素的状态变化所消耗的成本向量综合成一个总的成本向量，这就是该入口元素的总调整效率向量。为了方便地构造这种总调整效率向量，先作一个前提假设：在所处理的状态制约系统中，各个元素的调整效率之间无交互作用，即对系统中的任何两个元素si和s j，对si状态的任何调整都不会改变s j在当前状态下的调整效率，只要元素sj的当前状态不发生改变。

在这样的假设前提下，有：

设入口元素sk的当前调整能力向量为c k＝(Δt 1，Δt 2，…，Δt n)，其中所引起的元素si的状态变化量为Δti，发生Δti所需要消耗的成本向量为b i＝(bi1，bi2，…，bim)，显然，当前总调整效率向量b hk 所表示的是入口元素e k在当前状态下，其状态值变化一个单位，并且引起系统中各个被它制约的元素的状态发生一定变化时(究竟发生多大变化，取决于相应的制约函数的形式)，所需要消耗的成本所组成的向量。在对状态制约系统的状态进行调整时，只能对各个入口元素进行调整，这样，为了在调整时达到优化，即为了能够花费最小的成本而取得最大的调整效果，就需要确定各个入口元素的调整幅度和调整顺序。在实现这方面的优化算法时，入口元素的当前调整能力向量和当前总调整效率向量起重要作用。

设关卡元素sk的当前调整能力向量为c k＝(Δt 1，Δt 2，…，Δt n)，其中所引起的元素si的状态变化量为Δti，发生Δti 所需要消耗的成本向量为

称为关卡元素的当前总调整效率向量。

显然，当前总调整效率向量b hk 所表示的是关卡元素的状态发生一定变化时，所需消耗成本所组成的向量。在对状态制约系统的状态进行调整时，只能对各个关卡元素进行调整。关卡元素的当前调整能力向量和当前总调整效率向量对系统的优化起到非常重要的作用。