国际经验与中国实践：资本流动波动测算方法

如何测算国际资本流动波动是研究特定类型资本流动波动影响因素的关键，参照现有文献，主要有4种测量方法，分别是以滚动窗口计算的资本流动标准差作为波动值、用GARCH（1，1）模型估计的标准差作为波动值、用ARIMA模型估计标准差作为波动值以及用ARIMA（1，1，0）条件选择模型估计标准差作为波动值，具体如下。

（一）以滚动窗口标准差计算资本流动波动

Neumann（2009），IMF（2007）在计算国际资本流动波动时运用年度数据使用这种基于滚动窗口得出的标准差作为国际资本流动波动值。计算方法如下：

其中i表示国家，t表示年度，n表示4个季度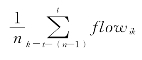，，即4个季度的资本流动平均值。这种用标准差表示资本流动波动的方法比较有效，但是也存在一些缺陷，具体如下：

①开始时样本存在数据丢失现象；

②σit具有很强的连续性，和前期相关性较大，这可能会导致内生性和序列相关性问题；

③从模型可以看出，和被模型赋予了相同的权重，这就意味着不同时期的资本流动权重相同，这是过度平滑波动的表现。与其他测量方式相比，当一个资本冲击发生时，此种计量方法算出的波动可能被低估，也可能被高估。

（二）以GARCH（1，1）模型估计的标准差作为资本流动波动

第二种替代的测量方法由Bollerslev（1986），Bekaert et al.（1997），Segot（2009）提出，使用GARCH（1，1）模型估计波动。估计的过程如下所示：

在这个模型里，εit是一个高斯白噪声过程，是对应的条件方差。此种方法虽然在某些方面强于滚动窗口计算的资本流动标准差，但是也存在以下一些缺点：

①数据的缺失会使得GARCH估计出现收敛误差，特别是在样本前期对小样本的最大似然估计存在偏差。

②平稳性和正相关性估计要求α1＋α2＜1，α0＞0，α1＞0和α2＞0。对于没有满足上述条件的国家，测量结果无效。(www.xing528.com)

③在某些情况下，残差不存在ARCH效应，意味着使用GARCH模型出错。

（三）以ARIMA模型估计的标准差作为资本流动波动

Broto（2011）基于Engle et al.（2008）运用ARIMA模型得出标准差作为波动测量结果的研究，考虑到宏观经济变量的频率低于金融变量，宏观经济变量具有不确定性，需要对每个变量进行建模，然后对取得的残差采取四季度滚动平均作为年度波动的平方。具体公式如下：

其中vitj表示t年j季i国资本流动的残差，的标准差即年度资本流动波动结果，但是以上模型存在结果不稳定。

（四）以ARIMA条件选择模型估计的标准差作为资本流动波动

Pagliari et al.（2017）在Broto et al.（2011）的基础上，墙加了是否通过ARCH检验的条件，在此基础上采取后续不同的处理方式，同时估计值是对于数据进行ARIMA（1，1，0）条件模型估计后得到残差的标准差。首先，估计AR（1）过程中的残差：

其次，检测残差是否存在任何的ARCH效应。如果异方差的零假设被拒绝，则：

否则，条件波动的估计适合GARCH（1，1）模型对残差的估计，进行下列操作：

其中，εit是高斯白噪声过程，是条件方差。

ARIMA（1，1，0）条件选择模型得出的波动估计值，一方面有助于提高估计结果的稳定性；另一方面，打破了仅仅使用GARCH（1，1）有局限性的问题。因此本研究选用ARIMA（1，1，0）条件选择模型得出的标准差作为波动测量结果，从而更准确地计算波动结果。