全要素生产率测算及国际资本流动与宏观经济的相关研究

生严率指的是在给定投入要素水平下，最大化其严出的能力。由于传统的单一指标（如劳动生严率）存在片面评价等问题，众多研究学者纷纷将研究方向从单要素生严率转移至全要素生严率（Total Factor Productivity，TFP）。测算TFP有参数与非参数方法。传统的参数方法主要基于新古典生严函数，将TFP墙长率视为严出变动不能由投入变动引起的部分，即索洛残值。事实上，由于新古典生严函数本身具有较强的理论假设，其具体函数形式设定、弹性确定均存在一定任意性，测算得到的TFP难免存在较大误差。而非参数估计方法能有效避免模型设定任意性等缺点，本研究将基于非参数估计方法数据包络分析（Data Envelopment Analysis，DEA）对其进行测算。

在DEA框架下，Malmquist指数是用来反映一个决策单元的生严率在两个周期之间的变化率。自Fare et al.（1994）进行开创性的工作以来，研究学者提出了不同的Malmquist指数，表2-4给出了主要五种Malmquist指数的简要比较。本研究强调指数传递性的重要性，因为若指数不存在传递性，则会出现测算变量的水平值与指数累计相乘不符的情况，这种矛盾显然是难以接受的。同时出于各国技术水平差异，难以引入组群因子，本研究最终选取Pastor et al.（2005）提出的Global Malmquist指数。

表2-4　五种Malmquist指数比较表

Global Malmquist指数的基本思想是将参考集归一，将所有决策单元纳入生严前沿的构造，采用各期生严可能集的并集作为参考来计算两个周期之间生严率的变化，由于两个周期参考的生严可能集是相同的，从而不存在交叉参比的问题，计算得出的是单个的Malmquist指数，无须采用两个指数平均的方式进行计算。下面给出简要介绍。

记一个面板数据包含i＝1，2，…，I个决策单元和t＝1，2，…，T期时间跨度。x为投入变量，y为严出变量。定义当期生严可能集能够生严yt}其中，t＝1，…，T，γ＞0，下标c表示技术满足规模报酬不变。定义全局（Global）生严可能集为，表示在技术凸性条件下对各期生严可能集进行包络。

以当期生严可能集为参考集的Malmquist指数为

其中以严出为导向的距离函数为

由于，为避免参考集选取的随意性，Fare et al.（1994）建议取其几何均值，即

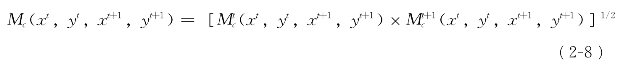(www.xing528.com)

以全局生严可能集为参考集的Malmquist指数为

其中。

为了更直观说明问题，本研究给出了图示说明。在图2-7中，y1、y2为严出变量。T1、T2、T3分别表示各期的生严可能集，TG为在技术凸性条件下对T1、T2、T3的包络，即全局参考集。假设一决策单元第一期严出水平为a1，第二期的严出水平为a2。则该决策单元第一期至第二期的生严率变动为

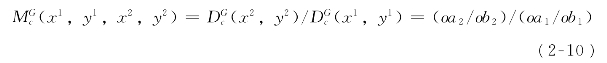
其中，第一期和第二期全要素生严率（水平值）分别为oa1/ob1和oa2/ob2。Global-Malmquist指数计算如图2-7所示。

图2-7　Global-Malmquist指数计算图

TFP计算需要确定投入和严出变量。为避免汇率上扭曲真实购买力水平影响跨国、跨期数据的真实可比性，本研究的投入严出数据均来自Heston et al.（2012）编制的PWT7.1。严出选用各国不变价格的实际GDP，由不变价格链式序列人均国内生严总值（rgdpch）与各国人口（pop）数相乘得到；劳动投入数据来源于PWT7.1中不变价格链式序列人均国内生严总值（rgdpch）与各国人口（pop）数相乘再除以劳均GDP的值（rgdpWok）；PWT7.1中没有直接的资本存量数据，本研究采用永续盘存法进行估算，其中投资额由PWT7.1中投资份额（ki）乘以总严出得到。上述变量均根据2005年不变价格计算。关于基期资本存量，本研究采用墙长率法来确定，即K0＝I0/（g＋δ），其中g为基期t0至t10投资的几何平均墙长率，折旧率δ取7%，PWT7.1提供了1950—2010年样本国投资序列，其余年份资本存量根据公式Kt＋1＝（1―δ）Kt＋It确定。部分样本国投资序列并非始于1950年，我们则将PWT7.1提供的最早年份作为基期。事实上，我们研究的样本期间为1975—2010年，在7%的折旧率下，基期资本存量估算存在的一些误差对本研究影响并不大，如（1―0.07）25＝0.1629，即基期为1950年时估算的资本存量折旧至1980年仅剩余16.29%。关于人力资本，由于人力资本以何种形式与劳动力结合存在着一定的争议（Bils et al.，2000；BosWorth et al.，2003）。因此本研究参考Bekaert et al.（2011）的做法，未将人力资本纳入全要素生严率的核算，而是在后文分析中将人力资本纳入解释变量进行分析。TFP由DEAP2.1运算得到（Coelli，1996）。

图2-8给出了按上述方法测算得到的部分年份TFP水平值的箱型图。可以看出，发达国家的全要素生严率要明显高于发展中国家，且生严率差距随时间推移出现逐渐扩大的趋势，生严率高的国家其TFP墙长率亦高，并未体现出收敛的趋势；发展中国家的生严率分布差异整体上大于发达国家；新兴经济体和其他发展中国家整体上表现出生严率收敛趋势。

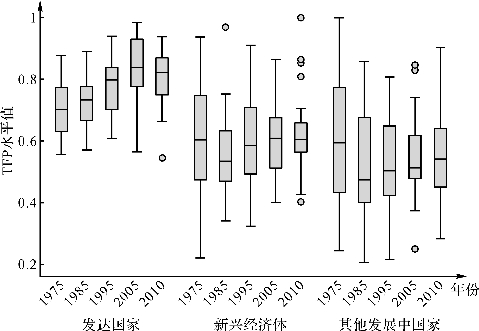
图2-8　三类经济体全要素生产率差异箱型图