金融期权风险管理实例

10.1.4.1　期权价格的决定

在金融期权交易中，期权价格的决定是一个最重要的问题。期权交易主要有以下几个关系与要素，它们相互联系、互相作用。

1.执行价格、市场价格和内在价值之间的关系

执行价格（Exercise Price）与市场价格（Market Price）是影响期权价格的两个重要因素，即执行价格不同的期权合约，按照与当时市场价格的差别而有不同的期权价格。

期权合约本身所具有的内在价值（Intrinsic Value）也是金融期权交易中的一个非常重要的问题。内在价值一般是指美式期权购买者在有效期内任一时点上或欧式期权购买者在到期日当天立即执行该期权所能获得的全部收益 （即买方盈利），它反映了期权本身所具有的内在价值。期权的内在价值PK、执行价格PE与市场价格PM三者有着一定的联系。

若忽略交易成本，则对看涨期权、看跌期权的买方有以下情形，即

看涨期权：PK＝PM-PE

看跌期权：PK＝PE-PM

由此，执行价格（PE）越高，在一定的市场价格（PM）下看涨期权的内在价值（PK）越低，看跌期权的内在价值（PK）越大。事实上，对看涨期权而言，PE越高，在有效期内（PM-PE）增大的可能性越小；而对看跌期权而言，PE越高，在有效期内（PE-PM）增大的可能性越大。于是，在看涨期权时，有

若PM-PE＞0，则PK＞0，表明内在价值为实值；

若PM-PE＜0，则PK＜0，表明内在价值为虚值；

若PM-PE＝0，则PK＝0，表明内在价值为零（即两平）。

例如，英镑与美元市场汇率（PM）为GBP 1＝USD 1.525 6，某投资者持有执行价格（PE）为GBP 1＝USD 1.456 5 的英镑看涨期权，则该投资者只要执行该期权，每英镑就可得到0.07 美元的收益，即英镑看涨期权的内在价值为0.07 美元；假如此英镑市场汇率为GBP 1＝USD 1.435 6，比执行汇率低0.02 美元，则该看涨期权的内在价值为虚值，即没有内在价值；两平的情形就是此英镑市场汇率恰好为GBP 1＝USD 1.456 5。同样，在多头看跌期权时，所有情况正好相反。

现将上述分析结果列表（见表10-4）并做图（见图10-6）。

表10-4　期权内在价值

图10-6　期权内在价值示意图

2.时间价值

期权除具有内在价值外，还具有时间价值（Time Value）。期权的时间价值是指期权买方在希望随时间延长使市场价格的变动有可能让期权增值时愿意支付的期权费（Option Premium）。

一般地，期权的时间价值是期权价格超过其内在价值的部分，即

时间价值＝期权价格-内在价值

上式意味着，对于一个还没有到到期日的美式期权来说，它在某日所具有的总价值（即期权价格上限）等于它具有的内在价值与时间价值之和，这表明了期权价格上限既高于期权的内在价值，也高于期权的时间价值。

3.期权费

期权费是影响期权的最重要因素。它的多少既取决于执行价格的高低，也取决于期权时间价值的大小。

对看涨期权来说，期权费是随着执行价格的增加而减少的；而对看跌期权来说，期权费则是随着执行价格的增加而增加。期权费的多少还取决于金融市场行情。当期权交易的金融商品市场价格上涨时，购买看涨期权的期权费就增加，而购买看跌期权的期权费会下降；反之，当期权交易的金融商品市场价格下跌时，购买看涨期权的期权费就下降，而购买看跌期权的期权费会增加。

对时间价值而言，无论是看涨期权还是看跌期权，时间价值越大，期权费越高；当时间价值为零时，便得到了期权费的下限；当两平时，由于内在价值等于零，故时间价值达到了最大值。

4.利率

影响期权交易的另一个要素是利率（Interest），特别是短期市场无风险利率。利率的变动对期权交易的影响较为复杂。例如，在买进股票看涨期权时，由于不需要支付股票的全部价款，只需支付远低于股票实际价格的期权费，而在到期时按照期权执行价格购买股票，这样期权费与实际购买股票的费用之间便存在一个差额，在未到期日之前，期权买方可以从这一差额的投资中得到利息收益，市场利率越高，利息收益越大，这个延期支付也就越有价值。因此，市场无风险利率越高，期权价格越高；但另一方面，在利率提高时，股票价格一般会下跌，这样可能会使以股票为标的的看涨期权的内在价值减小。这同时在一定程度上影响了金融期权市场的交易。因此，利率对期权价格的影响，应做具体的深入分析。

5.市场价格波动

在期权交易中，市场价格波动（也称市场易变性）是影响期权价格的重要因素，但它不具有方向性，即它没有反映市场价格上升（牛市）或下跌（熊市）的趋势。从概率统计来看，市场价格波动是一个方差（或标准差），是前两个观察值价格之比的对数的标准差，一般用正态分布来反映市场价格的分布情况，其公式为

式中，R 为市场上所观察的原始价格P 转换而成的对数收益率，即R1＝ln （Pt/Pt-1）。

由于实际观察到的数据序列有时不够完整，因此可用Rt的修正值代入公式来计算σ。其中，（m 为两个观察价格Pt与Pt-1间隔的天数）。

一般来说，市场价格波动范围越大，期权持有者转向实值或者实值增大而使盈利的机会越多，卖方承担的风险就越大，因而期权价格将升高。这里要注意，期权价格的确定与预期收益无直接关系，它取决于价格本身的波动性大小。例如，对股票期权来说，两种股票的预期收益率不同，但可能具有相同的期权价格。当然，股票的预期收益率会影响股票市场价格变化，从而间接影响到股票期权的内在价值。

6.剩余时间

剩余时间是指期权买卖日至期权到期日的时间。一般来说，距到期时间越长，使用期权的机会越多，期权买方获利的可能性越高，卖方承担的风险也越大。此外，买方在未来要支付的执行价格的现值与距到期日的时间成反比，因而期权价格越高，附着于期权上的潜在性货币价值就越大，即超出的价值就越大，这一超出的价值也就是时间价值。

伴随期权合约剩余时间缩短，期权的时间价值也随之衰减，直至为零。这是因为，转向实值或者实值增大的机会也伴随期权合约剩余时间的缩短而减少，即买方获利的机会也在减少，期权价格作为对期权卖方所承担风险的补偿也在逐步降低，于是时间价值也将逐步减小，如图10-7 所示。

图10-7　剩余时间长短与时间价值的关系

7.时间价值与市场价格、执行价格之间的关系

时间价值除了与剩余时间有关以外，还与标的的市场价格有关。对看涨期权或看跌期权而言，只要期权为深度虚值，则标的资产的足够改变使期权成为实值的可能性非常小，投资者一般不愿为时间价值付出很多；但是当期权为深度实值时，内在价值会相当大，投资者将不愿意为期权付出超过内在价值过多的部分。这样，在所有其他条件相同的情况下，可以预料当期权是两平（即PM＝PE）时，其时间价值最大。

时间价值与标的市场价格的关系如图10-8 所示。

图10-8　时间价值与标的市场价格的关系

事实上，由于时间价值等于期权价格减去内在价值，因此当期权是两平（即PM＝PE）时，内在价值达到最小值零，此时时间价值取得了最大值并等于期权价格。

总之，影响期权交易的要素很多且很复杂。每个要素在不同的时间和条件下对期权价格的影响不同，它们之间既紧密联系又相互抵销。例如，期权价格是随着执行价格而变化，与时间价值也密切相关，同时利率涨跌的变化对期权价格产生不同方向的影响，而期权价格又与利率有关的市场价格波动有关等。因此，期权价格是一个多元函数，自变量包括执行价格、市场价格、利率、剩余时间与市场价格波动等因素。

10.1.4.2　Black-Scholes 期权定价模型

1.Black-Scholes 微分方程

设f 是股票期权价格，并考虑卖出一份买入期权和买入数量为股票的证券组合π，其组合价值为

式中，-f 为卖出一份衍生证券；为买入份股票。

Δt 时间以后，π 的变化为

将Black-Scholes 数学表达式的离散形式代入上式，并注意股价遵循布朗运动，则有

ΔPM＝μPMΔt＋σPMΔz

化简后，可以得到

由于上式不再含有Δz，经Δt 后证券组合π 必定没有风险，因此证券组合的瞬时收益率一定与其短期无风险证券收益率相等，即

Δπ＝rπΔt （r 为无风险利率）

将π＝-f＋·PM和Δπ＝代入上式，可得

这就是Black-Scholes 微分方程，式（10-4）在推导的过程中是基于以下假设的：

（1）股票价格遵循dx＝adt＋bdz 描述的ITO 过程。

（2）允许使用全部所得卖空衍生证券。

（3）市场没有摩擦（即没有交易费或税收），证券高度可分（即可将证券分割为可以计价的单位供每位投资者交易）。

（4）衍生证券有效期内没有红利支付。

（5）不存在无风险套利机会，即市场越有效，套利机会越少。

（6）证券交易在价格和时间上是连续的。

（7）无风险利率r 为常数，且对所有到期日都相同。

2.风险中性定价

上面的几条假设属于风险中性性质，是为求解Black-Scholes 微分方程方便而做的人为假设，大大简化了风险中性定价。并且无论有无风险，此微分方程的解均有效。

在风险中性时，欧式看涨期权到期日与看跌期权到期日的期望值分别为

欧式看涨期权的价值为

欧式看跌期权的价值为

式中，PT为到期日T 期权商品的市场价格；PE为期权商品的执行价格；r 为无风险利率；t为现在时刻，T-t 表示距到期日的时间（即剩余到期日），其也可以用一年的一定比例表示。

在式（10-7）和式（10-8）中，如果T＝t，则表示看涨期权与看跌期权到期日时的期权价值，即为式（10-5）与式（10-6）的情形。

3.无红利的B1ack-Scholes 资产期权定价公式

对看涨期权的价格来说，在风险中性时，因对数收益率RT＝lnPT- lnPM服从于，故

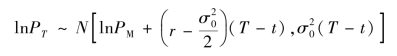
即lnPT服从均值为、方差为的正态分布，这表明PT具有对数正态分布。

令，则有

式中，f（PT）是PT的密度函数。

因为lnPT～N（m，σ2）（期权商品市价变化具有对数正态分布特征），这里，m＝lnPM＋，σ2＝，故有

由于

因此，有

若有红利K 支付，则式（10-9）可以调整为

该式为有红利的Black-Scholes 资产期权定价公式，其中

式中，PM为期权商品现价；N（d1）与N（d2）均是标准正态分布函数值；σ 是期权商品价格波动性（即标准差）；PEe-r（T-t）是PE的现值，但它是使用连续型贴现率，若采用离散型贴现率，则变为PE/（1＋r）（T-t）；r 与PE含义同前。

用类似方法可以求出看跌期权定价公式，即

式中，r、PE、PM、d1、d2、T-t 同前面看涨期权定价公式中的含义相同。

另外，由于看跌期权与看涨期权的平价关系（即在无套利机会时看跌与看涨期权的均衡水平价格关系）为

PM＝PE＋C-P

移项后，得

P＝PE＋C-PM

考虑货币的时间价值，上式变为

P＝C-PM＋PEe-r(T-t)

将上式代入看涨期权定价公式中，也可以得到

由N（-d）＝1-N（d）进一步可以得到P＝PEe-r（T-t）N（-d2）-PMN（-d1），这与前面推导的结论完全一致。

Black-Scholes 期权定价公式精确地给出了期权价格，在理论与实践中具有广泛的应用价值。它精确描述了期权价格是期权商品市场价格（PM）、执行价格（PE）、价格波动性（σ）、无风险利率（r）以及距到期日时间长度（T-t）的五元函数。

在两个期权价格公式中，只有一个价格波动性参数σ 需要通过最近6 个月至1年内的历史股价数据进行经验估计，其余四个变量值均较容易获取。

从看涨期权定价公式可以看到：

（1）由于无风险利率可作为购买期权的机会成本，因此在看涨期权中，无风险利率越高，机会成本越大，要求期权的收益率越高，进而期权价格也越高。

（2）距到期日时间越长，期权价格越高。

（3）期权执行价格越高，期权价格越低。

（4）市场价格越高，期权价格越高。

（5）市场价格波动越大，期权价格越大。

同样，可以得出看跌期权中的这些变量与看涨期权价格的关系，有些与看涨期权中的关系相同（如第（2）条等），但有些与看涨期权中关系不同（如第（1）条等）。

10.1.4.3　金融期权的风险管理策略

金融期权作为一种衍生工具，在期权交易中存在着一定风险，然而它正是通过其自身带有的风险同现货市场中的风险相对冲来实现金融期权的风险管理功能。

1.单种期权的风险指标及其指标间关系

1）Delta 与Delta 管理

期权的Delta（Δ）是指当期货等基础资产价格发生微小变化时，期权价格的变化程度，是期权价格曲线的斜率，即

Δ＝期权价格变化/期货等基础资产价格变化

计算Delta（Δ）时，期权价格仅受期货等基础资产价格影响，而将其他影响期权价格的因子视为常数。由Black-Scholes 期权定价公式，可得

式中，C 是看涨期权的期权费。

或

(www.xing528.com)

式中，P 是看跌期权的期权费。

图10-9　期权Delta 与股价关系

（a）看涨期权Delta；（b）看跌期权Delta

图10-9（a）和图10-9（b）分别描述了看涨期权与看跌期权中Delta 与股价的关系。在图10-9 中，-1.0＜Δ＜1.0，描述对于看涨期权，当基础资产价格超过执行价格很多（即严重溢价），Delta 值接近1 时，表示的是一个极度增值的看涨期权价格上涨，其将完全由基础资产价格上涨反映出来；当基础资产价格低于执行价格很多（即严重损价），Delta 值接近0 时，表示的是一个极度减值的看涨期权，此时随着基础资产价格的降低，期权价格降低幅度将很小。同样可以描述看跌期权的严重溢价与严重损价情形，此时Delta 值分别接近于-1 与0。

当基础资产价格接近执行价格时，看涨期权Delta 值约等于0.5，看跌期权Delta 值大约为-0.5，即平价时看涨期权的Delta 值为0.5，看跌期权的Delta 值为-0.5。由于-1.0＜Δ＜1.0，故表明期权价格变化小于基础资产价格变化。例如，一份看涨期权的Delta 值为0.8，这表示基础资产价格每上涨1 美元，其期权费相应增加0.8 美元。若一份看跌期权的Delta 值为-0.8，则表示基础资产价格每上涨1 美元，其期权费相应减少0.8美元。

Delta 运用于风险管理时便构成Delta 管理，可直接分析各类资产Delta 的加总来衡量特定资产组合头寸牛市或熊市的强弱程度。

从Delta 概念可引出Delta 保值概念并以此降低或转移风险。Delta 保值是企图构造投资组合，使组合的各组成部分的Delta 相互冲销，进而使整个组合的Delta 值为0 （称为中性），以达到对冲保值目的。构成资产组合的各类资产Delta 加总就是所谓的头寸Delta。若交易者持有100 份Delta 值为0.64 的买入期权合同，则他需卖出64 份期货合同，使100 份这种期权合同的价值变动与64 份同种期货合同的价值变动相等，即所谓的Delta 避险。同样，若交易者持有100 份Delta 值为0.16 的卖出期权合同，则他需买进16 份期货合同。

Delta 保值策略的实际效果取决于期货价格等基础资产价格变动的途径及频率。随着变动频率增加，Delta 保值的效果也会随着增加。如果这种变动可以连续地进行，则交易者可利用Delta 量化期权头寸中的内在风险的各个侧面，在认定这种风险可以接受时，交易者就会停止这种变动，使Delta 值的波动控制在一定范围之内。

【例10-1】某股票现价为40 美元，股价波动性为每年55%，利率为6%。某投资者卖出了一个关于股票的3 个月后到期的看涨期权，执行价格为30 美元。该投资者决定对此头寸进行保值，买进一个执行价格为40 美元的同期限的看涨期权。试利用Delta 进行期权头寸的对冲分析。

解：由已知条件与Delta 公式，可以分别算出：

（1）卖出执行价格为30 美元的看涨期权的Delta 值为-0.892 2；

（2）买进执行价格为40 美元的看涨期权的Delta 值为0.576 1。

于是，Delta 总头寸为（-0.892 2）＋0.576 1＝-0.316 1，它意味着这个头寸在股价不变或上升情况下，依然有遭受损失的风险。为改善这个保值头寸效果，可以再买进执行价格为40 美元的看涨期权，让Delta 值接近0 以达到组合Delta 为中性的效果，即股价每上涨1 美元时，整个组合后的期权费几乎不变。

对于一个执行价格为30 美元的看涨期权空头来说，应该买进执行价格为40 美元的看涨期权数量为0.892 2÷0.576 1≈1.548。在这样的保值策略下，如果股价大幅度上升，所面临的风险就会大大低于以股票建立保值头寸的情况。

一般运用Delta 管理来降低或转移风险的做法有：出售持有股票（即兑现）；买入股票看跌期权；卖出股票看涨期权以及买入股票看跌期权、卖出股票看涨期权进行某种程度的综合等。一般地，利用Delta 套期保值的期权交易者，须持有与其期权合同头寸相反的期货合同等头寸，期货合同等数量由Delta 值确定。

【例10-2】假定在1月26 日，某资产组合管理者持有10 000 股IBM 公司股票，现行股价为每股33 美元。市场条件的变化使该资产管理者决定将手中持有的股票风险降低至原先风险水平的90%。

IBM 股票头寸Delta 值是10 000，每一股股票代表一个Delta 点。现在的目标是将头寸Delta 值降低到90%，即9 000，此时可供选择的方法有以下三种：

（1）出售1 000 股IBM 股票（即兑现）；

（2）买入看跌期权；

（3）卖出看涨期权。

出售股票是一种可以采用的手段，但交易所收取佣金较高，且资产管理者需要再买入股票时，又需要一笔较高的佣金。买入看跌期权不利之处在于需要支付一笔期权费。因此，资产管理者常常采用第三种方法。

如果IBM 股票的3月期看涨期权执行价格为35 美元，每股期权费2 美元，Delta 值为0.441，资产管理者就会决定出售N 份（每份100 股）看涨期权合约，以让头寸Delta 值减少1 000，具体列式为

1×10 000-(0.441×N×100)＝9 000

因为1 000＝44.1N，故N＝22.68≈23 （份），即卖售23 份看涨期权合约后获得期权收入为2×23×100＝4 600 （美元）。现在头寸Delta 值为10 000-0.441×2 300＝8 986，这与初始头寸Delta 值10 000 相比减少了1 014，现在资产组合具有89.86%的牛市倾向。

一周以后，IBM 股票市场价格为32.5 美元，执行价格为35 美元的3月期看涨期权的Delta 值为0.404，头寸Delta 值也从8 986 变为9 071，即

1×10 000-(0.404×2 300)＝9 071

若资产管理者打算进一步降低持有IBM 股票的风险，使其降低到原先风险水平的50%，要达到这种目标，仍然有以下三种办法可以选择，即

（1）出售9 071-5 000＝4 071 （股）IBM 股票；

（2）买入看跌期权；

（3）卖出更多的看涨期权。

该资产管理者决定采用卖出更多的看涨期权这种办法。如果执行价格为35 美元的3月期看涨期权现在的出售价格为每股1.625 美元，则出售77 份（9 071-0.404×77×100＝5 960）这种看涨期权合约，可获得1.625×7 700≈12 513 （美元）的收入，现在的头寸Delta 为

(1×10 000)-(0.404×10 000)＝5 960

与初始状态相比，现在的资产头寸具有59.60%牛市倾向。持有IBM 股票仍呈现牛市倾向，但是如果继续出售看涨期权，则风险可能更大。因为这些看涨期权属于无抵补看涨期权。在这种情况下，资产管理者不再会出售看涨期权，而改为买入看跌期权方法来降低风险。

如果执行价格为30 美元的4月份到期的看跌期权，期权费为每股1.95 美元，Delta值为-0.310。这样，需要买入31 份看跌期权合约，才可以使头寸Delta 值变为

（10 000-4 040）-0.310×100×31＝4 999 （即达到投资者所要求的水平）

从表10-5 可以看出，与初始状态相比，现在牛市倾向为49.99%，已达预期目标。

表10-5　IBM 股票头寸Delta 列表

在3月份期权到期日，IBM 股票价格为33 美元。持有IBM 股票的资产管理者出于种种考虑，决定使资产头寸恢复到原来的100%牛市倾向，即头寸Delta 值为10 000。执行价格为35 美元的3月期看涨期权到期时无价值。执行价格为30 美元的4月期看跌期权可以出售，则根据Black-Scholes 期权定价公式，可以得到这种看跌期权价值为0.96 美元。将案例分析中的有关收支列表，参见表10-6。

表10-6　期权交易收支情况

从本案例可以看出，由于空头看涨期权与多头看跌期权具有负数Delta 值，因此出售空头看涨期权或买入看跌期权可以降低资产组合所面临的风险。但是，如果资产组合的头寸Delta 值已经小于0，那么继续出售看涨期权或买入看跌期权将会增加市场风险。此时，可采用出售看涨期权办法来略微降低市场风险，同时获取一定数量的期权费收入。但如果要大幅度降低市场风险，则应该采用买入看跌期权办法，同时要支出一定数量的期权费。

鉴于上述分析，富有经验的投资者一般先会卖出足够多的看涨期权，然后将获取的期权费收入用于购买看跌期权的支出，这样既达到了投资者对头寸Delta 的目标，也可以少支出期权费。总之，须通过改变持有的期权头寸来维持一个适当的Delta 目标值。

2）Gamma （Γ）与风险管理

Gamma 是相应Delta 值的变化速率，即Delta 值相对于股价变动的敏感程度，用公式表示为

第一个等式表明，Γ 是Delta 对股价的一阶偏导数；第二个等式表明，Γ 也是期权价格对股价的二阶偏导数。如果一个期权有一个比较小的Gamma 值，则Delta 值会相对稳定，因而其Delta 保值效果也会好一些；反之，若Gamma 值较大，则反映了Delta 值对股价变动的敏感程度较大，即Delta 值相对不够稳定。

对于欧式期权来说，Gamma 值为

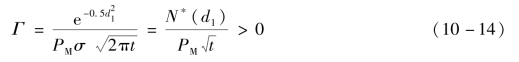
式中，d1＝；N*（ d1）＝；PM、PE、r、σ 和t 的含义与Black-Scholes 期权定价公式的含义相同。

【例10-3】某股票现价为50 美元，股价波动性为30%，无风险利率为5% （年率、连续复利），关于此股票的一个3月后到期的平价欧式看涨期权价格为3.27 美元，试求Delta值与Gamma 值。

解：由题意可知，PM＝50，PE＝3.27，r＝5%，σ＝0.30，t＝0.25年，得

Δcall＝0.562 5，Γ＝0.052 9

即股价上涨1 美元时，期权价格相应上涨0.562 5 美元；而当股价上涨1 美元时，Delta 值将增加0.052 9，所以新的Delta 值为

0.562 5＋0.052 9＝0.615 4

从欧式看涨期权的Γ 计算公式可以看出，Γ 值与到期日时间、d1、股价及股价波动性成反比。

一般来说，运用对Gamma 值进行经常性的调控构成Gamma 管理。Gamma 值大于0 来源于多头期权头寸，它表明当基础资产价格上涨时，Delta 值随之增加，期权资产变得更有牛市倾向；反之，当价格下降时，Delta 值随之减少，期权资产将会趋于熊市。空头期权头寸的Gamma 值一般小于0。

这样，当股价发生变动或随着时间的推移时，Gamma 可用来对期权资产组合调整的幅度进行估计。如果某种期权的Gamma 值接近于0，那么这种期权的Delta 值对股价的变动不会很敏感。

构成资产组合的各类资产Gamma 值加总起来就是头寸Gamma。当一个资产组合的Gamma 为0 时，称作Gamma 中性。

与期权头寸Delta 的对冲一样，交易者也往往利用Gamma 风险指标来量化其期权头寸中内在风险的各个侧面，以寻求建立最理想的保值头寸。但在实际中，交易费用的存在和信息的不充分，经常使修正保值头寸成本很高，效果也未必理想。

【例10-4】某股票现价为40 美元，股价波动性为每年55%，利率为6%。某投资者卖出了一个关于股票的3 个月后到期的看涨期权，执行价格为30 美元。该投资者决定对此头寸进行保值，买进一个执行价格为40 美元的同期限的看涨期权。试利用Gamma 进行期权头寸的对冲分析。

解：由已给条件，可计算出

（1）卖出执行价格为30 美元的看涨期权Gamma 值为-0.016 9；

（2）买进执行价格为40 美元的看涨期权Gamma 值为0.035 6。

因此，总头寸值为（-0.016 9）＋0.035 6＝0.018 7，比较接近0，进而反映出这种期权的Delta 值对股价变动的敏感性较低，即Delta 值会相对稳定。

3）Theta （θ）与风险管理

Theta 是指期权价格随时间变化的敏感程度，可表达为

它表明期权距离到期日会越来越短，而越是临近到期日期权的时间价值就越小。也就是说，随时间的推移，对多头期权头寸的持有者将日益不利，期权时间价值在逐日下降，所以对多头看涨期权或多头看跌期权的Theta 值为负数；相反，随时间的推移，期权出售者将越来越有利，因此空头看涨期权和空头看跌期权的Theta 值为正数。

具体计算Theta 值则可采用下面两个公式，即

（1）看涨期权：

（2）看跌期权：

式中，所有变量含义均与Black-Scholes 期权定价模型中变量的含义相同。

如果对Theta 计算公式进行变形如下，即

这样便可得到Theta 与Delta 之间的一个关系，即

构成资产组合的各类资产的Theta 值加总起来就是头寸Theta。当一个资产组合的Theta值为0 时，称作Theta 中性。与前面的期权头寸Delta、头寸Gamma 的对冲一样，也用于期权保值，关键仍是它们之间的构成比例。

4）Delta、Gamma 和Theta 之间关系

对于一个特定组合头寸，由前面给出的Black-Scholes 微分方程，Delta、Gamma 和Theta 之间关系满足下面关系式，即

式中，θ、r、PM、Δ、σ、Γ 含义同前；f 为该头寸的价值。

如果此头寸为Delta 中性，则有

它表明，当投资组合的Theta 值为较大的正数时，则相应地其Gamma 值为绝对值较大的负数。如果Delta 与Gamma 均为中性投资组合，则投资组合的Theta 也将接近于rf。

以上讨论了单种期权的几个主要风险指标，还有一些风险指标如用来衡量期权价格相对于执行价格波动性敏感程度的Vega （Λ）指标、用来衡量期权价格相对于无风险利率敏感程度的ρ 指标等。计算这些风险指标的变化值，以便于当损失值超过可以接受的临界值时，对投资组合加以调整。

2.资产组合的风险指标

在单种期权风险指标基础上，从资产组合的整体去考虑各风险指标，有利于消除由于分别控制单种期权风险指标而带来的负面影响。例如，看涨期权的Delta 是正值，看跌期权的Delta 是负值。如果考虑这两种不同期权的投资组合，则它们之间可以部分地相互抵销些。因此，投资者利用n 种期权合约构造投资组合以达到特定的效果远好于通过单种期权达到的效果。

下面介绍同一基础交易物不同期权的投资组合，这里将不同资产的期权当成一个组合来考虑。

假设某投资者以n1份某种看涨期权、n2份另一种看涨期权、m1份某种看跌期权、m2份另一种看跌期权构造组合头寸，则对应此头寸的价值为

式中，c1、c2为看涨期权合约价格；p1、p2为看跌期权合约价格。对应于这个头寸，其五个风险指标Δ、Γ、θ、Λ、ρ 分别为

Δ＝n1Δc1＋n2Δc2＋m1Δp1＋m2Δp2

Γ＝n1Γc1＋n2Γc2＋m1Γp1＋m2Γp2

θ＝n1θc1＋n2θc2＋m1θp1＋m2θp2

Λ＝n1Λc1＋n2Λc2＋m1Λp1＋m2Λp2

ρ＝n1ρc1＋n2ρc2＋m1ρp1＋m2ρp2

投资者在构造组合头寸时，以自己的收益及风险偏好来建立风险指标为特定值的组合。例如，如果投资者想完全抵销价格波动风险，则可以选择一个Delta 中性与Gamma 中性的投资组合；如果投资者认为股价会上涨，则可以选择一个高Delta 值的头寸；反之，如果投资者认为股价会下跌，则可以选择一个低Delta 值的头寸等。总之，只要投资者对以上风险指标有清楚的了解，就可根据其掌握信息充分的程度，选择一个最适合自己的投资组合。

3.期权弹性与期权杠杆效应

看涨期权的弹性E 定义为期权价值变化相对于股价变化的敏感程度，其计算公式为

显然，E 值越大，期权价值变化速率就越高于股价变化速率；反之，E 值越小，期权价值变化速率越低于股价变化速率。当E＝1 时，表明两者变化的速率完全相同。

由Δ＝，将其代入式（10-18），可得

该式描述了看涨期权弹性E 与Delta 值的关系，当PM与c 固定时，E 与Delta 成正比例。由Black-Scholes 期权定价公式可知，在一时点上一个看涨期权头寸相当于一个包含一部分以借款买进该股票的投资组合，通过动态调整，这个投资组合损益情况与该看涨期权损益情况相同，因而可以称这个投资组合为该期权的复制头寸。于是，通过分析该复制头寸的损益能够掌握看涨期权的风险收益情况。

如果复制头寸是部分由借入款构造的，则称此为期权杠杆效应。下面，简要探讨一下期权弹性与杠杆效应之间的内在关系。

假设以W 表示投资者自有资金量，Q 表示借入的资金量，λ 表示杠杆率，则

可以看出，杠杆率λ＞1。λ 越大，意味着在自有资金量一定时借入资金量越小；反之，λ越小，则借入资金量越多。如果某投资者自有资金为W，以无风险利率r 借入资金Q，且全部投入收益率为RP的有风险组合中，由APT^[3]模型可知，其收益率RQ为

RQ＝λRP＋(1-λ)r

此组合的预期收益率及其方差分别为

E(RQ)＝λE(RP)＋(1-λ)r

相应地，有

Δ＝βQ＝λβP

这里，βQ与βP分别是借入资金与组合的β系数。

由于看涨期权损益与复制头寸损益一样，因此一个看涨期权杠杆率为

有λ＝E，即复制头寸杠杆率等于期权弹性。杠杆率越大，期权弹性越高，期权杠杆价值变化率（即期权风险）也就越大。反之，杠杆率越小，期权弹性越低，期权价值变化率也就越小。

这样，期权弹性除可用E＝表示外，还可用E＝λ 来表示，这两者均在期权风险管理中发挥一定的作用。它们的取值大小依赖于每个投资者合适的选择。

由上面得出的Δ＝λβP，知道期权的Delta 值是期权弹性与有风险组合P 的β 系数之积。

4.改变市场风险的期货期权方法

期货和期权两者如果能以某种恰当的比例组合起来，便可以控制所面临的市场风险。一般来说，期货看涨期权持有者有权以事先确定的价格买入预定数额的期货合约，期货看跌期权持有者则有权以事先确定的价格卖出预定数额的期货合约。

【例10-5】假定某资产管理者的一笔股票资产价值为1.15亿美元，β 系数为0.98，S＆P 500 期货合约指数值为365.00，试用期货和期权方法求出最优组合。

解：S＆P 500 以500 美元为约定乘数来计算期货合约价格，所以，一份期货合约的价值为500 ×365.00＝182 500 （美元），1.15亿美元的股票资产等值于115 000 000 ÷182 500＝630 （份）期货合约。如果波动性σ 为15%，无风险利率为8%，现行期货价格为365，则可以选择355 份S＆P 500 看跌期权和275 份S＆P 500 看涨期权，组合成630 份距到期日还有100 天的期权合约。这样，由Black-Scholes 期权定价公式，分别估算出看涨期权费是7.11美元，其Delta 值是0.372；看跌期权费是6.83 美元，其Delta 值是-0.340.则保值总头寸Delta 为0.032，期权交易净收入为46 940 美元。

需要注意的是，如果1.15亿美元股票的市场风险发生变化，那么用以保值的S＆P 500期货看跌期权、期货看涨期权的最优组合构成也会相应变动。