中美中学理科教材比较：数与运算差异揭秘

在“数与代数”领域的处理问题上，中美两国采取了不同的方式。中国《数学课程标准》把“数与代数”领域作为一个整体给出标准，其优点是有助于沟通数与代数两者之间的联系，在教学上有助于整体把握；美国《共同核心标准》把“数与代数”领域分为“数与运算”和“代数”两部分，并分别给出标准，这种安排的优点是有助于两个教学内容的细化和深入，缺点是两者之间的联系体现得不够充分。为了使两国标准能够在一个平台上比较，我们把中国《数学课程标准》中的“数与代数”领域划分为“数与运算”和“代数”两个部分。下面分别从“数与运算”“代数”“函数”三个部分对两国的内容标准进行比较研究。

1.“数与运算”内容标准的比较

表1-13　“数与运算”内容标准比较

续表

表1-13是中美两国“数与运算”内容标准的对照表，从中可以看出两国《课程标准》在制定理念上是有所不同的。中国《数学课程标准》的教学目标的重心在基础知识和基本技能上，美国《共同核心标准》的教学目标的重心在知识的理解和问题解决上。从内容的广度上看，中国《数学课程标准》包含系统的无理数知识，而美国《共同核心标准》则仅仅包含少量的无理数知识，在中学年级只是实现对无理数的一个初步理解的目的。从内容的深度上看，中国《数学课程标准》以实数为教学重点，而美国《共同核心标准》以有理数为教学重点，教学要求相对来说较我国浅一些。

2.“代数”内容标准的比较

表1-14　“代数”内容标准比较

表1-14是中、美两国“代数”内容标准的对照表，如上表所示，美国《共同核心标准》在这一领域提出了四个标准，概括地说是“模式、关系和函数的理解”“代数符号的应用”“数学建模”“函数变化的分析”四个部分。中国《数学课程标准》这一领域分为“代数式”“方程与不等式”和“函数”三个部分。美国《共同核心标准》的四个部分是并列的，并且贯穿了整个基础教育的各个学段，中国《数学课程标准》的三个部分是按照知识的系统扩展来安排的，这种安排有助于学生掌握系统的知识和技能。在这一学段两国要实现的基本目标是一致的，即完成代数的常量教学向函数教学的过渡。但在实现的方法上，两国标准有所不同，中国《数学课程标准》的实现途径为：代数式——方程与不等式——函数；美国《共同核心标准》的实现途径为：模式——关系——函数。中国《数学课程标准》的实现途径有利于学生掌握系统的知识和技能，学生的分析能力和运算能力较强。美国《共同核心标准》的实现途径有助于学生的应用意识的培养，有利于知识的迁移，从而有利于学生创新能力的培养。美国《共同核心标准》通过“模式”的引入真正实现了抽象数学与现实的联系，把传统的代数内容延伸到了学生的生活空间，相比之下，中国《数学课程标准》的延展性有待于进一步加强。(www.xing528.com)

3.“函数”内容标准的比较

美国方面的课程，我们选择由美国加利福尼亚州一家公司出版的中学数学教材作为代表，在美国的使用具有较强的广泛性；中国方面，我们选择上教版的中学数学教材作为中国数学课程的代表。美国、中国教材“函数”内容的相应章节选取见表1-15所示。

表1-15　美国、中国“函数”内容标准比较

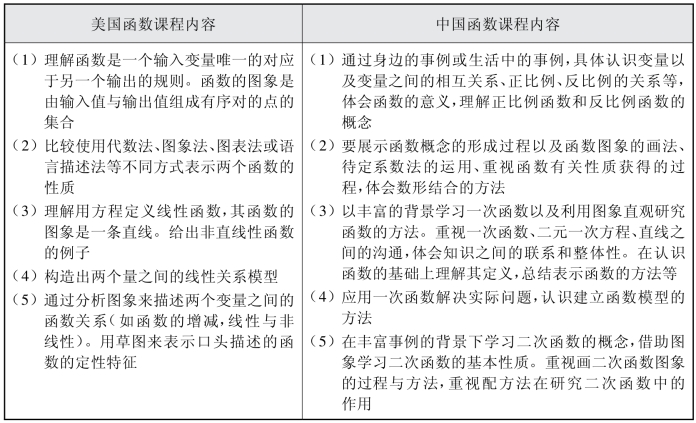
通过表1-15我们可以发现，两国《课程标准》中对“函数”内容的设置有着许多共同点，也存在着一些差异，从影响数学问题设置的角度我们进行分析这些异同点，具体体现如表1-16所示。

表1-16　美国、中国“函数”内容标准的异同

续表

从上表两国函数课程内容的异同点来看，两国数学课程对函数的课程目标大致相当，都十分强调对于函数概念的理解，也都提到了学习函数一些常用的方法技巧，并且也都注重函数与现实生活之间的关联和函数的应用。但是，美国对于函数的课程内容相对较少，因此其课程目标自然比我国的课程目标低，但对于线性函数的课程深度较大，如已经提及函数与集合（上海在高中才开始学习这一模块的内容）的联系，比较注重对于函数图象的理解（如增减性、线性和非线性等）；我国数学课程对函数包含的数学思想方法的掌握，这一点与前文提到的《上海数学课程标准》的总目标中的强调掌握基础，学会基本技能和方法等要求相一致。