《数学教学设计与案例分析》：设计意图的形成

设计意图应该是教学设计者根据教学目标而设定的在具体教学设计环节的整体或者每一个步骤的意图，应该是整体教学目标的细化落实工作。设计意图可以分为整体设计意图和过程设计意图，这两个设计意图应该前后呼应，紧扣教学目标。教学设计意图是教学设计者的创意体现，也是设计教学过程的“幕后台词”，是教学理念的具体落实。

（一）整体设计意图

整体的教学设计意图是设计者根据教学总体目标以及本节课的具体目标而对本节课的设计预想。它的形成主要依据以下四个方面：一是课程标准所提出的教学总目标和本节课的具体教学目标，二是设计者已有的教学理念和教学经验，三是本节课的教学任务，四是学生的具体情况。设计者对整节课的知识、技能的分布情况应该有一个清晰的认识，对近现代数学教育理论有一定的了解，能够从教育理论的高度把握整节课的设计意图。

关于整体设计意图，我们有这么几点想法：一是要有整体的战略思想，把握整体结构的内核，紧扣重点，攻克难点，不为细枝末节所困扰；二是要符合学生的认知规律，尊重学生的思维起点，问题设计的入口要宽，所设计的问题尽量为所有学生都愿意参与并“多少能够说出个一二”的内容；三是要尽量对学生进行科学方法论的教育，展示人类研究问题的策略与思维过程；四是要关注“动机”“方法”“落实”的数学课堂教学设计三要素，前后呼应，一气呵成；五是要留有余地，慎重考虑课堂的意外，预设好基本的对策。关于整体的教学设计意图，我们认为，在每章或每个单元的第一节课的引入设计环节上对这个意图要特别关注。另外，要关注章节之间的衔接设计，包括每节课的各个环节的设计衔接工作，这些“衔接台词”就是宏观思维的具体体现。

（二）过程设计意图

过程设计意图是相对于整体设计意图而言的，理论上说，过程设计意图应该服从于整体设计意图，要为整体教学布局服务。但是，过程设计有时又可以为整体设计提供修正信息，可以影响整体设计意图，甚至推翻整体的设计思路。

1.课堂引入过程的设计意图

课堂引入就像整体战略序幕的拉开，是培养宏观思维很好的途径之一，也是培养学生捕捉信息敏感性的重要途径，有经验的教师会对这个环节非常重视。这个环节的意图形成主要考虑这样两个因素：一是本节课在所在章节的位置及作用，若是该章节的第一节课，则引入环节应该有整章的引入的任务，之后才是本节课的引入。二是本节课的内容如果是本章节首节课的后续课程，则可以依照本章引言的布局来个前呼后应，从而顺利引出课堂教学内容，巩固学生对整章内容的结构把握。当然，某些课可以创设一些生活情境引入，这是为了让学生体会学习这些数学知识的实用性和重要性，提高学生的数学应用意识和数学学习兴趣，但不要忘记让学生明白本节课在整章节的地位和作用，要“扭紧”本章节的“知识链”，“一环紧扣一环”。其实，课堂引入过程的设计意图不外乎有如下几个：一是引起学生的注意，迅速进入学习状态；二是激发学生的学习动机，提高其数学学习兴趣；三是培养学生的宏观思维，把握研究数学问题的科学方法；四是设立一些必要的情境，提高学生捕捉重要信息的敏锐性。

2.知识教学过程的设计意图

知识教学过程的设计意图离不开教师的“知识观”。对于知识产生的过程和知识本身的作用，不同的教师往往就有不同的看法。对于这个问题，我们有四点“分类式”的想法。

（1）知识产生的过程和知识本身的作用都很重要。例如，圆周角定理的发现、证明以及其本身在后续中的作用都很重要，教师不能犯“重结论、轻过程”或“重过程、轻结论”的毛病，有些教师往往认为该定理的证明过程需要不少的时间，假如三种情况都进行证明，则学生的练习时间就没有了，于是就往往把其证明过程给部分省略了，然后就让学生做有关圆周角定理应用的练习。其实，圆周角定理的教学是数学知识教学的“一道大餐”，省略或缩短过程的教学往往是得不偿失的。就圆周角定理而言，圆周角定理的发现过程教学充满着数学方法论的教育，其证明则涉及思路的剖析及分类等思想的教育，发现过程和结论证明都是数学教育很好的素材。

（2）知识产生的过程暂且不重要，但知识本身作为结论的作用则相对更重要。知识产生的过程暂且不重要，主要可能是基于知识产生过程的学习超越学生的学习能力、教育价值低、可操作性不强、减轻学生学习负担等原因考虑的。几千年的数学知识产生过程都让学生学习显然不现实，因此我们应该引导学生学习一些具有较大教育意义的知识产生过程，其余的要根据学生的特点，由他们“自助学习”。现在新课程的改革出现了“定理公理化”的现象，即以往老教材作为定理需要证明的，在新教材中往往就简单演示一下，学生只要觉得结论是正确的就可以了，这种做法或许就是新课程对知识产生过程的教育价值重新评估后的举措。例如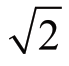，“是无理数”的教学，教师只需展示的近似值随精确度是无限不循环的过程即可，其证明过程若不是“超越了学生的学习能力”则也有“加重学生学习负担”之嫌，我们通过调查发现，绝大部分学生对“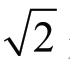是无理数”是深信不疑的。或许有些老师在担心，一些数学知识只关注其结论、忽视其过程的做法是否对学生培养理性精神是不利的？我们认为，这种担心在某种情况下是有一定道理的，一些知识的产生过程的教育价值也是需要进行学术界定的，这个讨论可能还是一个“永恒的课题”。

（3）知识产生的过程重要，但知识本身作为结论的作用则相对不重要。平面几何中很多证明题都是训练学生对平面几何知识的运用能力，这些证明题的结论本身也是知识，但这种知识作为结论显然就暂时不那么重要了。但在具体教学过程中，一些似乎不那么重要的结论，有些老师则往往把它捡起来成为“学生学习的宝贝”，加重了学生的记忆负担。例如，在立方体的平面展开图的教学中，对立方体展开后的各种情况，有些教师采取口诀，要求学生记住：“一四一、一三二、一在同层可任意；三个二、成阶梯，两个三、日状连，整体无田。”在和这些老师的交流中，他们的意思是：“口诀也好记，一旦考试中有这道题，学生就很快解决了。”我们在想：“假如考试考到的是一个无盖的立方体展开图，那会不会学生因为找不到口诀而放弃解题呢？或者，即使学生记住了，一旦在考试或练习中真的遇到了立方体的展开图，一些记住公式的学生很快就做出来，他们是否在增加记忆负担的同时也失去了一次空间想象力培养的训练机会？”我们曾经对来自不同学校的十几个初二学生进行采访，只有一个学校的老师没有进行这方面的“总结”，他们也根本不知道有这样的“口诀”，倒是老师有要求记住这一口诀的学生都记不住，有几个学生甚至说：“老师要求我记住，我一开始就不以为然，因为我只要想一下就可以了！”

现在有一些观念认为过程重要，主要指解题模式重要，亦即以往我们所说的题型教学。我们不否认题型教学在目前数学应试教育情况下的作用，但是数学问题是千变万化的，过于模式化而忽视思维过程的展示教学对学生的思维培养是有害的，因为一旦问题的条件发生微小的变化，很可能问题解决的方式就相差甚远，同时因为学生由于教师给予过多的模式而忽视了思维的锻炼，反而依赖于对问题解决过程的记忆上。我们这里所说的过程重要是指一些问题的解决过程的教学很能够锻炼我们学生的思维，增加学生的智慧，并不是指过程模式化的重要性。(www.xing528.com)

（4）知识产生的过程和知识本身作为结论的作用都暂且不重要。陈省身在回答梁东元对他的提问时说：“举个例子，大家也许知道有个拿破仑定理。据说这个定理和拿破仑有点关系。它的意思是说，任何一个三角形，各边上各作等边三角形，接下来将这三个三角形的重心连接起来，那么就必定是一个等边的三角形，各边上的等边三角形也可以朝里面作，于是可以得到两个解，像这样的数学，就不是好的数学，为什么？因为它难以有进一步的发展。”

我们认为，凡是数学都需要“人在动脑筋”，都具有“训练思维的作用”，但对于学生而言，他们的时间是宝贵的，应该让他们学习一些对培养他们的思维和能力具有很强迁移效果且结论对后续知识及现实实际都有重大作用的数学。在中小学数学中，针对中学生，一些数学知识及形成过程暂且不重要，对于他们的影响而言，有“坏”的一面：①结论并不重要，对以后学习并不起多少的平台作用，就像陈省身所说的，“难以有进一步的发展”，记住反而加重记忆负担。②过程也不重要，有些甚至使学生对数学产生误解。例如，观察数列的前五项，写出这个数列的第六项：61，52，63，94，46， ________，答案是18。理由是把这个数列的每一项数字的个位数与十位数对调：16，25，36，49，64，显然，按照这个规律，显然接下去是81，然后调换个位数与十位数，即得到答案。按照现在时髦的语言，这是“脑筋急转弯”！我们认为，这是“整人的数学”，绝对是对数学学习者的误导！要判定一个数学知识的好坏，我们可以从这样的几个方面考虑：①数学知识的发展性。即该数学知识是否能够成为后续数学学习的好平台，是否是构筑其他有用数学知识的好基础。②数学知识的教育性。知识本身的形成过程能够起到培养学生各方面的能力、陶冶学生的情操、提高学生的数学学习兴趣等作用。③数学知识的应用性。除了成为其他数学知识学习的平台或者能够直接教育学生外，有些数学知识还能够在其他学科或者实际生活中有很好的应用，是解决实际问题的“好工具”。④数学知识的文化性。一些数学知识能够在社会文化中起到一定的作用，这些数学知识承载着文化传播的任务，这种数学我们也认为是好数学。说到这里，我们得提一下几何教学改革。布尔巴基学派的代表人物之一狄多涅在《我们应该讲授新数学吗？》一文中提到过“欧几里得滚蛋”的说法，试图推倒欧氏几何在数学课程中的基础地位。当时，有一种观点认为，一些高深的几何把学生的大量时间耗费在其中，而对现实生活急需的数学却在教学中视而不见的做法是不对的。近代数学教学的改革确实把几何学删除了不少，对几何学的作用在学术界中的争议还是很大的，今后估计也可能还有一个漫长的争议时间。按理说，知识产生的过程和知识本身作为结论的作用都暂且不重要的数学都应该淡出我们数学教学设计的视野，但在实际教学过程中，尤其是在应试教育环境下的我国的数学教学，却经常出现数学“使坏”的现象。例如，我们经常在一些初中试卷的试题中看到类似“的算术平方根是________” 的数学测试题。此类问题在考学生是否清楚“算术平方根”的概念的同时，还考学生的“脑筋急转弯”，这是何苦呢？难怪一些学生对数学敬而远之，充满厌恶感。

3.技能训练过程的设计意图

数学技能的训练过程的设计是我国数学教育工作者非常重视的话题，尤其是应试环境下的数学技能的教学设计。由于数学技能训练“扮演”着“巩固数学知识”和“提高数学能力”的“双重衔接身份”，这个环节自然受到师生的重视，当然，一些在重大考试中经常用到的技能更是人们关注的话题，也成为一些教师的主要设计意图。关于数学技能的训练过程的设计意图有这么几个话题值得探讨。

（1）技能训练内容选择的设计意图。哪些内容能够成为学生训练技能的课题？哪些内容可以暂时不必成为学生训练技能的题材？这个问题不仅是每个教师而且是课程标准制定者和教材编写者认真思考的问题。例如，韦达定理（根与系数的关系）、十字相乘法就一直是课程改革的争议话题，到现在为止尚未有确定的结论。在我国，由于重大考试（如中考）的指挥作用，一些历年考题所涉及的数学技能自然成为数学教师的关注焦点，这些技能教师只要时间允许，是肯定会花精力去训练学生的，哪怕是训练过度也在所不惜，因为我们的一些老师坚信熟能生巧。

（2）技能训练过程的环节设计意图。数学技能训练过程的设计一般需要根据学生已有的认知水平、所训练的数学技能的特征、学生的心理状态等来进行。一般来说，数学技能的训练步骤有以下四个：①认知。教师进行必要的知识教学和技能示范，让学生了解所训练技能的内容，先把技能当作知识来进行学习。②模仿。依据教师示范来进行模仿，期间，教师进行必要的纠正与指导，尤其是针对后进生群体。③初步学会。学生可以脱离教师的指导，进行独立的练习，并通过校对答案来评价和反思自己进行的技能训练的成果。④学会。学生通过自己的独立练习，具备较高成功率地完成，还可以与其他已经掌握的数学技能进行比较与反思，为灵活性做好准备，试图向能力方向转移。尽管如此，不同教师的设计也有很大的差异性，其意图也是各不相同。例如，有的教师先提出训练目标，自己一开始不进行示范让学生模仿，而是先让学生自己摸索和感悟，教师在一边观察，适时对个别学生进行点拨，然后针对学生比较困难的地方进行集体点评和示范，这种“半自学型”的技能训练也是一种有益的尝试。又如，有的教师把要训练的技能的宏观思路与学生进行“商量”，然后再把“比较大”的技能分解为几个“小技能”让学生自己训练，甚至让学生自己“命题”来训练自己。一般来说，技能训练设计有两个主要的方向：①“摘香蕉理论”，其所提的数学技能目标先比较高一些，然后依据学生的情况降低训练目标，让学生通过努力能够完成，即让他们“跳一跳，够得着”而最终摘得“香蕉”。②“跳高理论”，该理论是先将技能训练的“门槛”降得很低，学生能够很快完成这些低高度的数学技能，而后再逐步提升技能训练的难度，直至学生完成有困难，教师再根据具体情况指导学生。这两种的技能训练设计可以根据具体的教学内容灵活选择，教师不妨都尝试一下，以比较教学效果。

（3）技能训练的后续配套设计意图。技能是知识的运用与能力形成的中介，也是问题解决技巧的伏笔。一种数学技能的形成，是为后续的数学能力、数学问题解决的技巧奠定基础的，是否在后续的教学内容中设置与前面的技能训练相配套的相关教学设计，要依据整体的教学目标及教学的具体情况而定。例如，解二元一次方程组的技能完成后，是否让学生继续“乘胜追击”地学习三元一次方程组、四元一次方程组甚至多元一次方程组？当然，另一条后续路径是设计让学生学习二元多次方程组，甚至是多元多次方程组。在数学技能的后续配套教学设计时，有这么一种现象很值得我们探究：针对数学技能的“极端”情景，该如何处理？例如，解一元一次不等式时，一般教师的设计是很忌讳出现未知数最后“消失”的情景。例如，解不等式：x+1＞x－1。我们曾经对此和一些已经学习了一元一次不等式解法的七年级学生进行“试验”，结果，有的学生说：“找不到未知数，说明这个不等式无解。”也有的学生说：“找不到未知数，说明这不是一元一次不等式。”更多的学生是茫然不知所措。他们不知道该如何下结论，因为这种现象是他们从来没有见到过的。其实，为了完善学生的认知结构，对于一些学有余力的学生，在数学技能的后续配套设计中应该不失时机地让他们接触某些数学技能的“极端”情况，以提高他们分析问题和解决问题的能力，更加认清这些数学技能的本质。例如，针对不等式x+1＞x－1，当教师问学生：“什么是不等式的解？”当学生回答出：“满足不等式的一切实数就是不等式的解”时，他们很可能会“恍然大悟”：原来一切实数都满足该不等式！

4.例题讲解过程的设计意图

在数学教学设计过程中，针对例题的教学设计往往是一些优秀数学教师最为讲究的主题之一，但对于一些新教师，恐怕不一定有很高的认识，为此，我们在这里做一些讨论。

（1）例题选择的意图必须十分明确，这是例题的讲解及处理的前提。一般说来，例题的选择意图应该突出这样的几个主题：①前面所学的知识（数学概念、公式、法则、定理、公理及思想方法等）的巩固。②为形成或巩固数学技能所做的示范或加强。③提醒学生数学学习中可能存在的某些缺陷。④针对学生各种能力（包括数学应用能力）的培养。⑤进行某些数学思想方法的渗透或教育。值得一提的是，一些教师由于不是十分明确课本所设置的例题意图，往往采取两种极端的做法：一是按部就班，照样画葫芦地完成例题的讲解；二是推倒重来，另外自己寻找例题。针对这两种极端做法，我们认为需要认真思考。前一种往往是教师“懒惰”或“不自信”所造成的，当然，一些教师“吃透”课本作者的意图也可能会这样做。后一种往往是教师有些“教学经验”后的做法。其实，“吃透”课本作者的意图，认真完成课本例题的教育功能应该是我们数学教学的“主流”做法，但按部就班、不越雷池半步的做法也很值得商榷。因为我们的教学对象是千差万别的，不同时期的教学任务也不尽相同，适度调配（例如把课本个别例题作为课堂练习等）或补充课本的例题也是允许的，只要能够根据学生及当时的具体情况灵活变化即可。但是在对课本例题进行改动时，必须慎重又慎重，因为课本作者的权威性也不容忽视，他们的安排往往自有他们的道理，他们在编书的时候也是经过慎重考虑的。至于那些对课本例题视而不见的做法，我们认为是不负责任的，不值得提倡。

（2）数学例题一旦选择后，教学设计就得有这样几个方面的考虑：一是如何引出例题，二是如何实现例题的教育功能，三是如何根据课堂进行实际调配例题的处理时间，四是如何设计例题讲解完毕的后续教育问题。这些方面的意图应该非常明确。例如，新课引出例题一般都是为巩固新学知识服务的，一些学生刚学习了新知识，脑子里往往形成了定式，以为老师所举的例题肯定是采取刚学习过的方法，因此往往就按部就班地按照刚学习的内容和方法进行解题。其实，我们有些老师在选择例题的时候也是基于这样考虑的，往往在举出例题之前讲了类似这样的一句话：“我们刚才学了……下面我们就用它去解决以下的问题……”这些暗示性十足的语言无疑加重了学生的思维定式。其实在一些基础知识刚讲解完毕后，所举的例子应该有一个甄别何时运用这些知识去解决问题的引出设计。就等比数列求和公式的教学而言，在学习等比数列的求和公式后，教师在运用等比数列求和公式的例子之前，可以设置这样的引题：“求下列各式的和：①1+2+4+8；②1+2+4+5+8+16+32+64。”让一些不假思索就套用等比数列求和公式的学生“碰一下壁”，使他们懂得：何时才使用等比数列求和公式，用等比数列求和公式应该注意哪些事项等。又如，一个例题的教育功能有多样，是否都需要挖掘？如何把这个例题的教育功能发挥得“淋漓尽致”？在有限的教学时间能够办到吗？就一题多解、一题多变而言，这个问题很值得我们思考。我们有些教师往往处于一种两难的境界：一方面觉得例题的有些教育功能浪费可惜，另一方面感觉时间太有限。方均斌曾经发表过一篇文章，^[1]对挖掘课本知识的抉择及策略等问题，提出这样的观点：一是“典型”“适时”“有度”地挖掘，充分调动学生的积极性：①“挖”得典型，减轻负担。②把握时机，恰到好处。③点到为止，留有余地。二是讲究有策略地挖掘，发展学生的创造潜能，采用“迫挖术”“回味术”“归纳术”“搭梯术”，进行诱挖。其实，对例题教育功能的挖掘问题，说得可能容易，做起来就不那么轻松了。这就需要教师的经验积累、教学水平的提高以及教学观念的更新。

5.课堂结束过程的设计意图

对于课堂结束过程，一些老师虽然在教学设计中设置了该环节，但在具体教学操作时往往还是不太重视，即使有时精心设计了，但在教学操作时又往往由于时间不足而匆忙收尾。我们想在这里强调一下：学生的大部分学习时间以及将来成人后是靠自学的，我们数学教师对他们自学的自觉性以及自学能力的培养也负有不可推卸的责任。同时，学生学习的自我监控和元认知能力也是非常重要的，而在数学课堂结束过程的教学设计对这些因素的培养很重要，因此我们教师不应该忽视这个环节。数学课堂结束过程的设计应该具备这样几方面的意图：一是督促学生自我反思和监控本节课所学习的数学内容：哪些内容是学生自己感到疑惑或质疑的？学生自己是否已经掌握了教师所传授的数学知识和技能？哪些内容还可以继续深入探究？二是将本节课所传授的知识和技能进行“思维打包”，即将所传授的知识和技能结构化或模块化，便于学生系统掌握。三是延伸后续学习的任务，包括要完成的作业、要继续探究和反思的内容、下节课内容的预习任务等。四是后续学习时间的安排指导，即为学生课后的数学学习时间安排提供一个合理化建议。