异质性检验对于Meta分析的分析模型选择非常重要

异质性检验是Meta分析的必要工作，直接关系到后面分析模型的选择。该检验的基本思想是假如研究资料间的真实效应量一致，所有研究都来自同一个总体，那么实际效应量间的差异可认为是由抽样误差造成的，但若效应量间的差异过大，即这些变异不仅仅是抽样引起的，纳入Meta分析的各个独立研究可能来自不同的总体，而总体效应量间存在差异，则应考虑研究的异质性。

异质性检验常用方法是Q检验。

假设纳入的研究有k个。

1.建立检验假设，确定检验水准

H0：各纳入研究的效应指标相等，即θ1=θ2=…=θk

H1：各纳入研究的效应指标不等或不全相等

检验水准为α，一般为0.10。(www.xing528.com)

2.计算检验统计量Q值

Q服从于自由度为（k-1）的χ2分布。其中θi为第i个研究的效应量，θ为不同方法得到的合并效应量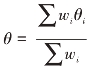，。wi为第i个研究的权重系数，不同方法其wi权重系数计算公式不一样。

3.确定P值，做出推断结论若Q≥x2α，k-1，则P≤α，拒绝H0、接受H1，可以认为各研究的效应指标不相同，即各研究间存在异质性，这些研究来自2个或多个不同的总体；若Q＜x2α，k-1，则P＞α，不拒绝H0，尚不能认为各研究的效应指标不相同，即可以认为各研究间是同质的，这些研究来自同一个总体。

除了Q检验法以外，还可以通过I2统计量检验各研究间是否存在异质性，I2≤25%则异质性较小，25%＜I2＜50%则为中等度异质性，I2≥50%则研究结果间存在高度异质性。

对于叙述性综述，异质性有可能只是偶然，在综述中有一小部分研究难以调查解释。即使是在较全面的综述中，如果某篇研究未用通用格式处理数据同样难以说明异质性。