SAS数据集转换与效应量标准化的关键作用

基于SAS系统，各个统计学分析程序只能对SAS数据集中的数据进行处理，所以将数据转换成SAS数据集是SAS进行统计分析的基础。选取易于解释、能够准确反映不同研究间结局指标关联程度的合并效应量指标是实现Meta分析的关键。效应量指标的选择依据数据类型的不同而变化，故为实现结局的可解释性，组间比较及组间合并对不同研究效应指标进行标准化尤为重要。在社会科学和医学领域，最常用的标准化效应量指标包括标准化均数效应量（d）、相关系数（r）、r的Fisher转化值（z）及比值比的对数转化值（logOR）。对于连续型数据，常采用d作为效应量指标，其计算公式如下：

式中，MT为干预组效应量均数，MC为对照组效应量均数，Swithin为组内标准差。

式中nT、nC和ST、SC分别为干预组和对照组样本量及标准差。d值的抽样不一致性可用方差（v）进行解释，其计算公式如下：

如果研究的两组样本量已知，可以通过单个效应量值计算v值。因为d近似服从真实效应的正态分布，因此也可用效应量的95%可信区间、标准差、标准误计算v值。对于二分类数据，比值比的自然对数值（lg OR）是常用的效应量指标，其计算公式如下：

式中，pT和pC分别指干预组和对照组的事件发生率，lgOR的抽样不一致性用其方差（v）表示，计算公式如下：

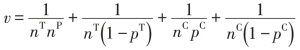
其中，nP和nC表示干预组和对照组的样本量。lgOR近似服从真实效应的正态分布，可用效应量的95%可信区间、标准差、标准误计算v值。OR指标系还包括相对危险度（relative risk，RR）和风险差（risk difference，RD），对于二分类数据效应指标测量的具体论述参考专业统计教材。对于连续型变量效应量结局指标，相关和相关系数也常被作为效应量指标。鉴于相关系数多数情况下不服从正态分布，因此通常将其经过Fisher转换（z），使其近似服从正态分布，具体转化公式如下：

式中，r为相关系数，不同类型检验对应r的计算参见专业统计教材。z值的抽样不一致性用其方差（v）表示，计算如下：

式中，n为研究样本量，该值也服从于其真实效应的正态分布，也可通过d和lg OR的v转化公式计算抽样不一致性方差。尽管对于不同数据类型合并选取不同的效应指标，然而各效应指标可以实现相互转化。lg OR及相应方差（vlgOR）与d值及对应方差（vd）相互转化公式如下：

r及对应方差（vr）转化为d值及（vd）公式如下：

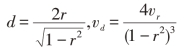(www.xing528.com)

d值及vd转化为r及vr公式如下：

式中，a表示校正因子，其值决定于两组样本量，。

基于本次示例数据的类型（二分类数据），使用前需要先行将效应量（effect size，es）对应转化为宏参数effect type效应指标所对应的lg OR值，标准误（SE）转化为方差（v）（v=SE2）。表7-8为示例数据转换完成后，录入命令如下：

表7-8　示例数据

data yxtx1；

input es v；

cards；

0.015 0.003136

-0.035 0.011236

-0.174 2.099601

-0.009 0.358801

-0.105 0.3249

；

run；

至此，以“yxtx1”为名的SAS数据集就被建立了。需要注意的是，标点符号均为英文状态下输入。