高考数学能力题解答攻略

知识结构

命题方向

数学能力题常常是高考试卷中的把关题和压轴题，在高考中举足轻重．高考的区分层次和选拔功能主要靠这类题型来完成预设目标．近几年高考数学能力题已由单纯的知识叠加型转化为知识、方法和能力综合型，尤其是创新能力型试题．能力题是高考数学试题的精华部分，具有知识容量大、解题方法多、能力要求高、突显数学思想方法的运用以及要求考生具有一定的创新意识和创新能力等特点．如何解答高考数学能力题？笔者建议：一是要进一步加强双基训练；二是注重数学思想和方法的理解和掌握；三是注重数学能力（阅读理解能力，独立获取知识能力，探究与创新能力）的培养与训练，四是采取避实就虚化整为零，各个击破分步得分的策略．

例题选讲

一、阅读理解能力

阅读理解能力是指通过阅读获取信息的能力，包括理解阅读材料中重要概念或句子的含义；筛选并整合图表、文字等阅读材料的主要信息细节；分析题意、把握关键词、归纳内容要点，理清思路，确定解题方案，实现数学建模．

例题1 某中学生在制作纸模过程中需要A，B两种规格的小卡纸，现有甲、乙两种大小不同的卡纸可供选择，每张卡纸可同时截得A，B两种规格的小卡纸的块数如下表，现需A、B两种规格的小卡纸分别为4，7块，所需甲、乙两种大小不同的卡纸的张数分别为m，n（m，n为整数），则m＋n的最小值为（　）．

A．2 B．3

C．4 D．5

图1

二、空间想象能力

空间想象力是人们对客观事物的空间形式（空间几何形体）进行观察、分析、认知的抽象思维能力，它主要包括下面三个方面的内容：（1）能根据空间几何形体或根据表述几何形体的语言、符号，在大脑中展现出相应的空间几何图形，并能正确想象其直观图．（2）能根据直观图，在大脑中展现出直观图表现的几何形体及其组成部分的形状、位置关系和数量关系．（3）能对头脑中已有的空间几何形体进行分解、组合，产生新的空间几何形体，并正确分析其位置关系和数量关系．培养学生的空间想象力是中学数学教学的主要任务之一，同时也是难点之一．

例题2 已知圆锥的侧面展开图是一个半圆，它被过底面中心O1且平行于母线AB的平面所截，若截面与圆锥侧面的交线是焦参数（焦点到准线的距离）为p的抛物线．

（1）求圆锥的母线与底面所成的角；

（2）求圆锥的全面积．

解：（1）设圆锥的底面半径为R，母线长为l．

由题意得：πl＝2πR，即，

所以母线和底面所成的角为60°．

（2）设截面与圆锥侧面的交线为MON，其中O为截面与AC的交点，则OO1∥AB且

如图2，在截面MON内，以OO1所在有向直线为y轴，O为原点，建立平面直角坐标系，则O为抛物线的顶点，所以抛物线方程为x2＝－2py，点N的坐标为（R，－R），代入方程得R2＝－2p（－R），得R＝2p，从而l＝2R＝4p．

图2

所以，圆锥的全面积为πRl＋πR2＝8πp2＋4πp2＝12πp2．

三、逻辑思维能力

逻辑思维能力是指正确、合理思考的能力，即对事物进行观察、比较、分析、综合、抽象、概括、判断、推理的能力，采用科学的逻辑方法，准确而有条理地表达自己思维过程的能力．它与形象思维能力截然不同．

逻辑思维能力不仅是学好数学必须具备的能力，也是学好其他学科，处理日常生活问题所必须的能力．数学是用数量关系（包括空间形式）反映客观世界的一门学科，逻辑性很强、很严密．

例题3 如图3，用35个单位正方形拼成一个矩形，点P1，P2，P3，P4以及四个标记为“▲”的点在正方形的顶点处，设集合Ω＝｛P1，P2，P3，P4｝，点P∈Ω，过点P作直线lP，使得不在lP上的“▲”的点分布在lP的两侧．用D1（lP）和D2（lP）分别表示lP一侧和另一侧的“▲”的点到lP的距离之和．若过点P的直线lP中有且只有一条满足D1（lP）＝D2（lP），则Ω中所有这样的点P为________．

图3

解：记“▲”的四个点为A，B，C，D，线段AB，BC，CD，DA的中点分别为点E，F，G，H，易知EFGH为平行四边形，如图4所示，四边形ABCD两组对边中点的连线交于点P2，则经过点P2的所有直线都是符合条件的直线lP．因此经过点P2的符合条件的直线lP有无数条；经过点P1，P3，P4的符合条件的直线lP各有1条，即直线P2P1，P2P3，P2P4．故Ω中所有这样的点P为点P1，P3，P4．

图4(www.xing528.com)

四、探索创新能力

创新能力是一种综合能力，是知识、能力、人格的有机融合和促进，是外在知识内化过程中多种智力因素契合、碰撞灵感火花的闪现，是指对自然界和社会中的数学现象具有好奇心，不断追求新知、独立思考，会从数学的角度发现和提出问题，并用数学方法加以探索、研究和解决．它包括数学创新欲望、数学创新情感、数学创新观念．

例题4 已知数列｛an｝是等差数列，其前n项和为Sn，若S4＝10，S13＝91．

（1）求Sn．

（2）若数列｛Mn｝满足条件：M1＝St1，当n≥2时，Mn＝Stn－Stn－1，其中数列｛tn｝单调递增，且t1＝1，tn∈N＊．

①试找出一组t2，t3，使得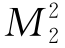＝M1·M3；

②证明：对于数列｛an｝，一定存在数列｛tn｝，使得数列｛Mn｝中的各数均为一个整数的平方．

所以Mn为一整数平方．

因此存在数列｛tn｝，使得数列｛Mn｝中的各数均为一个整数的平方．

五、独立获取知识能力

学习型问题是指对过去没有学习过的概念、法则、定理、公式或方法，在当前情境下通过阅读理解，即时学习，并运用其解决与之相关问题．学习型问题对培养学生的阅读理解能力、学会和会学、独立获取知识的能力以及创新精神和实践能力都是大有裨益的，因此成为全国各地高考数学命题追逐的热点之一．

根据f（x）的周期性，画出f（x）的图像如图5所示，显然①②③正确但④错误，故选C．

六、综合运用能力

数学综合性试题常常是指高考试卷中的把关题和压轴题．在高考中举足轻重，高考的区分层次和选拔使命主要靠这类题型来完成预设目标．目前的高考综合题已经由单纯的知识叠加型转化为知识、方法和能力综合型，尤其是创新能力型试题．综合题是高考数学试题的精华部分，具有知识容量大、解题方法多、能力要求高、突显数学思想方法的运用以及要求考生具有一定的创新意识和创新能力等特点．

（2）已知h（x）＝cos（x＋α）＋2cosx，且h（x）∈S，求其“相伴向量”的模；

跟踪训练

1．制定投资计划时，不仅要考虑可能获得的盈利，而且要考虑可能出现的亏损．某投资人打算投资甲、乙两个项目．根据预测，甲、乙项目可能的最大盈利率分别为100%和50%，可能的最大亏损率分别为30%和10%．投资人计划投资金额不超过10万元，要求确保可能的资金亏损不超过1．8万元．问投资人对甲、乙两个项目各投资多少万元，才能使可能的盈利最大？

2．已知满足条件x2＋y2≤1的点（x，y）构成的平面区域的面积为S1，满足条件［x］2＋［y］2≤1的点（x，y）构成的平面区域的面积为S2（其中［x］，［y］分别表示不大于x，y的最大整数），则点（S1，S2）一定在（　）．

A．直线y＝x左上方的区域内 B．直线y＝x上

C．直线y＝x右下方的区域内 D．直线x＋y＝7左下方的区域内

4．如果有穷数列a1，a2，a3，…，an（n为正整数）满足条件a1＝an，a2＝an－1，…，an＝a1，即ai＝an－i＋1（i＝1，2，…，n），我们称其为“对称数列”．例如，由组合数组成的数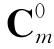列，，…，就是“对称数列”．

（1）设数列｛bn｝是项数为7的“对称数列”，其中b1，b2，b3，b4是等差数列，且b1＝2，b4＝11．依次写出｛bn｝的每一项；

（2）设数列｛cn｝是项数为2k－1（正整数k＞1）的“对称数列”，其中ck，ck＋1，…，c2k－1是首项为50，公差为－4的等差数列．记数列｛cn｝各项的和为S2k－1．当k为何值时，S2k－1取得最大值？并求出S2k－1的最大值；

（3）对于确定的正整数m＞1，写出所有项数不超过2m的“对称数列”，使得1，2，22，…，2 m－1依次是该数列中连续的项；当m＞1 500时，求其中一个“对称数列”前2 008项的和S2 008．

5．给定无穷数列｛an｝，若无穷数列｛bn｝满足：对任意n∈N＊，都有｜bn－an｜≤1，则称数列｛bn｝与｛an｝“接近”．

（1）设数列｛an｝是首项为1，公比为的等比数列，bn＝an＋1＋1，n∈N＊．判断数列｛bn｝是否与数列｛an｝接近，并说明理由；

（2）设数列｛an｝的前四项为a1＝1，a2＝2，a3＝4，a4＝8，数列｛bn｝是一个与数列｛an｝接近的数列，记集合M＝｛x｜x＝bi，i＝1，2，3，4｝，求M中元素的个数m；

（3）已知数列｛an｝是公差为d的等差数列，若存在数列｛bn｝满足：｛bn｝与｛an｝接近，且在b2－b1，b3－b2，…，b201－b200中至少有100个为正数，求d的取值范围．