数学专题攻略-上海新高考·数学　专题攻略

知识结构

命题方向

创新意识的激发，创新思维训练，创新能力的培养，是素质教育最具活力的课题，因此，近几年高考试题中出现了一些不拘泥于大纲，情景新颖，富有时代气息，有科学依据，切合实际，贴近生活的创新题．这类试题对培养学生的创新意识和创造性思维都是大有裨益的，因此在高考复习中要给予足够的重视．

例题精讲

一、观点创新型问题

观点创新就是以初等数学与高等数学的衔接点或高等数学的观点命题，而解决此问题必须具有一定的学习力，即独立获取知识的能力，以及灵活运用的能力，因此，在复习时应适度加强这方面的训练．

例题1 设S为复数集C的非空子集．若对任意x，y∈S，都有x＋y，x－y，xy∈S，则称S为封闭集．下列命题：

①集合S＝｛a＋bi｜a，b为整数，i为虚数单位｝为封闭集；

②若S为封闭集，则一定有0∈S；

③封闭集一定是无限集；

④若S为封闭集，则满足S⊆T⊆C的任意集合T也是封闭集．

其中真命题是________．（写出所有真命题的序号）

解：①中对任意x，y∈S，都有x＋y，x－y，xy∈S，所以集合S＝｛a＋bi｜a，b为整数，i为虚数单位｝为封闭集，①正确．

当S为封闭集时，因为x－y∈S，取x＝y，得0∈S，②正确．

对于集合S＝｛0｝，显然满足所有条件，但S是有限集，③错误．

取S＝｛0｝，T＝｛0，1｝，满足S⊆T⊆C，但由于0－1＝－1不属于T，故不是封闭集，④错误．

故答案为①②．

二、法则创新型问题

法则创新即问题中涉及以前未曾学过的运算法则，而解决此问题又必须用到这一法则，因此在解题之前，首先要对此进行阅读理解，即时学习，并加以灵活运用．

例题2 在实数集R中定义一种运算“＊”，具有性质：

①对任意a，b∈R，a＊b＝b＊a；

②对任意a∈R，a＊0＝a；

③对任意a，b，c∈R，（a＊b）＊c＝c＊（ab）＋（a＊c）＋（b＊c）－2C．

（1）求0＊2的值；

（2）求函数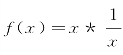（x＞0）的最小值．

解：根据条件③，对于任意的a，b，c有（a＊b）＊c＝c＊（ab）＋（a＊c）＋（b＊c）－2c，

取c＝0，得（a＊b）＊0＝0＊（ab）＋（a＊0）＋（b＊0）－2×0；

再根据条件①②知a＊0＝0＊a＝a对任意实数a都成立，代入上式可得

a＊b＝ab＋a＋b，这就是运算＊的定义．

将a＊b＝ab＋a＋b代入题干检验：a＊b＝b＊a，符合①；

a＊0＝a，符合②；

（a＊b）＊c＝（ab＋a＋b）＊c＝（ab＋a＋b）c＋（ab＋a＋b）＋c＝abc＋ac＋bc＋ab＋a＋b＋c，

c＊（ab）＋（a＊c）＋（b＊c）－2c＝（cab＋c＋ab）＋（ac＋a＋c）＋（bc＋b＋c）－2c＝abc＋ac＋bc＋ab＋a＋b＋c，

于是③也成立．所以a＊b＝ab＋a＋b是满足题意的运算．

（1）0＊2＝0×2＋0＋2＝2．

（2）f（x）＝x＊＋1，其最小值为3．

三、方法创新型问题

通过问题的解答提供一种全新的解法，通过对这一解法的理解，即时学习，即时应用．需要具备一定分析问题解决问题能力，及灵活运用知识方法的能力．

例题3 阅读不等式2x＋1＞3x的解法：

又因为3x＞0，所以2x＋1＞3x的解为x＜1．

解答下列问题：

（1）利用上面的方法解不等式32x2－x＋42x2－x≥72x2－x；

（2）试证明：方程3x＋4x＝5x有且仅有一个实数解x＝2．

四、定义创新型问题(www.xing528.com)

定义创新即问题中涉及以前未曾学过的概念，而解决此问题又必须用到这一概念，因此在解题之前，首先要对此进行阅读理解，即时学习，并加以灵活运用．

例题4 已知平面上的线段l及点P，在l上任取一点Q，线段PQ长度的最小值称为点P到线段l的距离，记作d（P，l）．

（1）求点P（1，1）到线段l：x－y－3＝0（3≤x≤5）的距离d（P，l）；

（2）设l是长为2的线段，求点集D＝｛P｜d（P，l）＝1｝所表示图形的面积；

（3）写出到两条线段l1，l2距离相等的点的集合Ω＝｛P｜d（P，l1）＝d（P，l2）｝，其中l1＝AB，l2＝CD，A，B，C，D是下列三组点中的一组．

①A（1，3），B（1，0），C（－1，3），D（－1，0）．

②A（1，3），B（1，0），C（－1，3），D（－1，－2）．

③A（0，1），B（0，0），C（0，0），D（2，0）．

解：（1）设Q（x，x－3）是线段l：x－y－3＝0（3≤x≤5）上一点，则｜PQ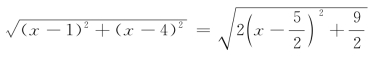｜＝（3≤x≤5），当x＝3时，d（P，l）＝｜PQ｜min＝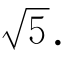

（2）设线段l的端点分别为A，B，以直线AB为x轴，AB的中点为原点建立直角坐标系，如图1，则A（－1，0），B（1，0），点集D由如下曲线围成：l1：y＝1（｜x｜≤1），l2：y＝－1（｜x｜≤1），C1：（x＋1）2＋y2＝1（x≤－1），C2：（x－1）2＋y2＝1（x≥1），其面积为S＝4＋π．

图1

（3）①选择A（1，3），B（1，0），C（－1，3），D（－1，0），如图2，则Ω＝｛（x，y）｜x＝0｝．

图2

②选择A（1，3），B（1，0），C（－1，3），D（－1，－2），如图3，则Ω＝｛（x，y）｜x＝0，y≥0｝∪｛（x，y）｜y2＝4x，－2≤y＜0｝∪｛（x，y）｜x＋y＋1＝0，x＞1｝．

图3

③选择A（0，1），B（0，0），C（0，0），D（2，0）．如图4，则Ω＝｛（x，y）｜x＝0，y＝0｝∪｛（x，y）｜y＝x，0＜x≤1｝∪｛（x，y）｜x2＝2y－1，1＜x≤2｝∪｛（x，y）｜4x－2y－3＝0，x＞2｝．

图4

五、探索创新型问题

探索创新型问题不仅选择范围广、覆盖面大，而且具有较强的综合性，对解题方法也有较高的要求，且必须有一定的预见性与灵活性，是训练和考查学生的思维能力、分析问题和解决问题能力的主要题型，是今后高考的主要考点之一．

（1）证明：数列｛bn｝是等比数列．

（2）求数列｛cn｝的通项公式．

（3）是否存在数列｛cn｝的不同项ci，cj，ck（i＜j＜k），使之成为等差数列？若存在请求出这样的不同项ci，cj，ck（i＜j＜k）；若不存在，请说明理由．

即2j－i＋1＝3j－i＋2k－i·3j－k，即2j－i＋1－2k－i·3j－k＝3j－i，左偶右奇不可能成立．所以假设不成立，这样三项不存在．

跟踪训练

1．设S是整数集Z的非空子集，如果对任意a，b∈S有ab∈S，则称S关于数的乘法是封闭的．若T，V是Z的两个不相交的非空子集，T∪V＝是Z且对任意a，b，c∈T有abc∈T，对任意x，y，z∈V有xyz∈V，有结论：

①T，V中至少有一个关于乘法是封闭的；

②T，V中至多有一个关于乘法是封闭的；

③T，V中有且只有一个关于乘法是封闭的；

④T，V中每一个关于乘法都是封闭的．

其中结论恒成立的是_________．

2．绝对值小于1的全体实数集合为S，在S中定义一种运算法则：“＊”使得a＊b＝．

（1）证明：如果a∈S，b∈S，则a＊b∈S；

（2）证明：结合律（a＊b）＊c＝a＊（b＊c）成立．

3．“已知关于x的不等式ax2－bx＋c＞0的解集为（1，2），解关于x的不等式cx2－bx＋a＞0”，有如下解决方案：

4．定义：设｛an｝是无穷数列，若存在正整数k使得对任意n∈N＊，均有an＋k＞an（an＋k＜an），则称数列｛an｝是近似递增（减）数列，其中k叫做近似递增（减）数列｛an｝的间隔数．

（1）若an＝n＋（－1）n，判断数列｛an｝是否为近似递增数列，并说明理由；

（2）已知数列｛an｝的通项公式为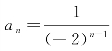＋a，其前n项的和为Sn，若2是近似递增数列｛Sn｝的间隔数，求a的取值范围；

（3）已知＋sinn，证明：数列｛an｝是近似递减数列，并且4是它的最小间隔数．

5．已知无穷数列｛an｝的各项都是正数，其前n项和为Sn，且满足：a1＝a，rSn＝anan＋1－1，其中a≠1，常数r∈N．

（1）求证：an＋2－an是一个定值．

（2）若数列｛an｝是一个周期数列（存在正整数T，使得对任意n∈N＊，都有an＋T＝an成立，则称数列｛an｝为周期数列，T为它的一个周期），求该数列的最小周期．

（3）若数列｛an｝是各项均为有理数的等差数列，cn＝2·3n－1（n∈N＊），问：数列｛cn｝中的所有项是否都是数列｛an｝中的项？若是，请说明理由；若不是，请举出反例．