知识结构
当一个数学问题所给出的对象难以用统一形式、方法研究时，只有将其分解成若干个小问题，通过对研究对象进行分类，然后对每一类分别进行研究，最后综合各类结果得到最终答案，这就是分类讨论的思想方法．分类讨论既是一种逻辑方法，也是一种重要的思想方法．这种思想在解决数学问题以及在学生的思维发展的过程中起着十分重要的作用．
一、分类讨论的作用
一是由大到小，即化整为零，实现复杂问题简单化；二是分类标准的划分相当于增加了一个已知条件，实现了有效增设方便求解之目的．
二、分类讨论依据
1．概念、定理、公式的分类；
2．存在不确定性元素，考虑分类讨论（题中含参数，且参数取值的不同会有不同的结果）；
3．存在关键型参变量，考虑分类讨论；
4．题中含有位置与形状不确定的图形，考虑分类讨论．
三、分类讨论的基本步骤
1．确定讨论对象；
2．确定分类标准；
3．逐类进行讨论；
4．归纳小结，综合结论．
命题方向
分类讨论思想贯穿高中学数学的各个部分，对培养学生思维的深刻性、严谨性、条理性，有着十分重要的作用，在高考试卷中占有着一定比例的分类讨论题，不仅具有良好的区分度，同时还可以进一步增强其选拔功能．因此成为近几年高考的主要考点之一．
例题精讲
一、存在不确定性元素，考虑分类讨论
二、对直线的斜率分类讨论
例题2 已知直线l经过点P（－3，1），且被圆x2＋y2＝25截的弦长为8，求直线l的方程．
解：如图1，当l垂直x轴时，设此直线l为AB，则｜AE｜2＝r2－｜OE｜2＝25－9＝16．
图1
由于｜AE｜＝4，则｜AB｜＝8，此时直线l的方程为x＝－3．
当l不垂直x轴时，直线l（直线CD）的方程为y－1＝k（x＋3），即kx－y＋3k＋1＝0，
则原点到直线的距离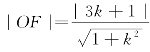
＝3，解得
，
则直线l的方程为4x－3y＋15＝0．
故直线l的方程为x＝－3或4x－3y＋15＝0．
例题3 已知数列｛an｝的通项公式为an＝an－1（其中a为非零常数）．(www.xing528.com)
（1）若数列｛an｝的各项和为5，求实数a的值；
（2）当a≠1时，设Sn＝a1－a2＋a3－a4＋…＋（－1）n－1 an，求
（3）实数a取（1）计算的结果，设bn＝10n－1 an2＋2n＋1，求数列｛bn｝中数值最大的项．
四、概念、性质的分类
当所给问题涉及的数学概念、性质，本身就是分类给出的，例如直线的斜率、圆锥曲线的概念等，首先考虑分类讨论．
例题4 设P（a，b）（b≠0）是平面直角坐标系xOy中的点，l是经过原点与点（1，b）的直线，记点Q是直线l与抛物线x2＝2py（p≠0）的异于原点的交点．
五、题中含有位置与形状不确定的图形
例题5 一圆柱的底面半径为R，上底面的一条弦CD的长为a（0＜a＜2R且a≠R），它与下底面的一条直径AB成60°的角，过点A和弦CD的截面与下底面成45°角，求圆柱的高．
解：设过点A和弦CD的截面为ACDE，则CD∥AE，所以∠BAE为CD与AB所成的角，所以∠BAE＝60°．设M为CD的中点，过点M作MP⊥下底面于点P，作PN垂直AE于点N，连结MN，易知∠MNP即为截面与底面所成的二面角，所以∠MNP＝45°，因此，在Rt△MNP中，MP＝NP．
图2
跟踪训练
1．设a为实数，函数f（x）＝x2＋｜x－a｜＋1，x∈R．
（1）讨论f（x）的奇偶性；
（2）求f（x）的最小值．
2．给定双曲线
＝1．
（1）过点A（2，1）的直线l与所给双曲线交于两点P1，P2，试求线段P1，P2的中点P的轨迹方程；
（2）过点B（1，1）能否作直线m，使m与所给的双曲线交于两点Q1，Q2，且点B是线段Q1Q2的中点？这样的直线如果存在，求出它的方程；如果不存在，说明理由．
3．若数列｛cn｝是递增数列，数列｛an｝满足：对任意n∈N＊，存在m∈N＊，使得
则称数列｛an｝是｛cn｝的“分隔数列”．
（1）设cn＝2n，an＝n＋1，证明：数列｛an｝是｛cn｝的“分隔数列”；
（2）设cn＝n－4，Sn是数列｛cn｝的前n项和，dn＝c3n－1，判断数列｛Sn｝是否是数列｛dn｝的“分隔数列”，并说明理由；
（3）设cn＝aqn－1，Tn是数列｛cn｝的前n项和，若数列｛Tn｝是｛cn｝的“分隔数列”，求实数a，q的取值范围．
4．已知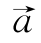
＝（k，y2），
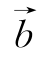＝（x2－1，k－4），且满足
＝1（k∈R）．
（1）求点P（x，y）的轨迹C的方程；
（2）若曲线C是椭圆，求k的取值范围；
（3）若曲线C是双曲线，且有一条渐近线的倾斜角为60°，求双曲线的方程．
5．如图，过双曲线
＝1（a＞0，b＞0）的左焦点的直线，交双曲线于A，B两点的直线有几条？
（第5题）
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
