数形结合：上海新高考数学专题攻略及历届高考试题分析

知识结构

命题方向

数形结合思想反映了数学研究的两个侧面，“数”是“形”的抽象概括，“形”是“数”的直观表现，它们有着密切的联系，在一定条件下可以相互转化，正如著名数学家华罗庚所说“数离形少直观，形离数难入微”，只有数形结合才能相映生辉——化抽象为直观、化直观为精确、化难为易、化繁为简，使问题得到不同程度的简化．总之，数形巧妙结合可以为问题的解决带来新的增长点．在历届高考试题中，都不同程度地对数形结合思想加以考查，在今后的高考中依旧是主要考点之一．

例题精讲

一、构造“距离”

二、构造斜率

例题2 已知实数x，y满足（x－6）2＋y2＝9，则的最大值是_________．

解：u＝表示动点B（x，y）与定点A（1，0）连线的斜率，如图2所示，当直线AB与圆（x－6）2＋y2＝9相切时，u取最大值，而｜AB｜2＝52－32＝16，即｜AB｜＝4，故umax＝tan∠BAC＝．

图2

三、构造直线

解：由g（x）＝f（x）－mx－m＝0，即f（x）＝m（x＋1），分别作出函数f（x）和y＝h（x）＝m（x＋1）的图像，如图3所示．

图3

由图像可知f（1）＝1，h（x）表示过定点A（－1，0）的直线，当h（x）过（1，1）时，，此时两个函数有两个交点，满足条件的m的取值范围是

当h（x）过（0，－2）时，h（0）＝－2，解得m＝－2，此时两个函数有两个交点．

当h（x）与f（x）相切时，两个函数只有一个交点，此时－3＝m（x＋1），即m（x＋1）2＋3（x＋1）－1＝0．

当m＝0时，x＝－，只有一解，

当m≠0，由Δ＝9＋4m＝0得m＝此时直线和f（x）相切，

所以要使函数有两个零点，则或，故选A．(www.xing528.com)

四、构造指对数曲线

例题4 若x1满足2x＋2x＝5，x2满足2x＋2log2（x－1）＝5，则x1＋x2＝（　）．

图4

五、构造三角函数

图5

六、构造圆锥曲线

跟踪训练

1．已知P是直线3x＋4y＋8＝0上的动点，PA，PB是圆x2＋y2－2x－2y＋1＝0的两条切线，A，B是切点，C是圆心，那么四边形PACB面积的最小值为________．

2．求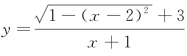的值域．

（第3题）

3．在等腰直角三角形ABC中，AB＝AC＝4，点P是边AB边上异于AB的一点，光线从点P出发，经BC，CA反射后又回到点P（如图），若光线QR经过△ABC的重心，则AP等于（　）．

4．已知实数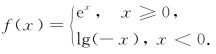若关于x的方程f2（x）＋f（x）＋t＝0有三个不同的实根，则t的取值范围为（　）．

A．（－∞，－2］ B．［1，＋∞）

C．［－2，1］ D．（－∞，－2］∪［1，＋∞）

5．方程＝｜2sin3x｜的实根的个数是（　）．

A．4 B．6 C．8 D．12

6．已知a＞0，a≠1，试求使方程loga（x－ak）＝loga2（x2－a2）有解的k的取值范围．