数学专题攻略：函数与方程思想

知识结构

命题方向

方程（不等式）与函数是相互联系的，在一定条件下可以相互转化，例如解方程f（x）＝0就是求函数的零点；解不等式f（x）＞g（x），就是当两个函数的函数值的大小关系确定后，求自变量的取值范围．函数方程（不等式）思想是实现问题转换的重要手段之一，因此，无论是过去还是将来都是高考试题考查的重点之一．

例题精讲

一、选定主元，构造函数

二、构造方程

例题2 已知抛物线y2＝2px，过抛物线的定点的弦OA和OB互相垂直，求以OA，OB为直径的两圆的另一交点Q的轨迹方程．

三、函数与方程、不等式的转化

例题3 已知函数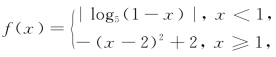则方程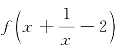＝a（a∈R）的实数根个数不可能为（　）．

A．5个 B．6个 C．7个 D．8个

解：依题意得，作出函数f（x）的图像，如图1所示．

图1

其他都是2个解，故一共有3×2＋1＝7（个）根．

2°当1＜a＜2时，有4个交点，则f（x）＝a有8个根．

3°当a＝2时，有3个交点，故f（x）＝a有6个根．

综上，只有A选项不可能，故选A．

四、利用函数与方程的性质解题

例题4 已知二次函数f（x）＝ax2＋bx（a，b为常数，且a≠0）满足条件：f（x－1）＝f（3－x）且方程f（x）＝2x有等根．

（1）求f（x）的解析式；

（2）是否存在实数m，n（m＜n），使f（x）定义域和值域分别为［m，n］和［4m，4n］，如果存在，求出m，n的值；如果不存在，说明理由．

解：（1）因为方程ax2＋bx＝2x有等根，所以Δ＝（b－2）2＝0，得b＝2．

五、函数思想在数列中的应用

例题5 设Sn是公差为d（d≠0）的无穷等差数列｛an｝的前n项和，则下列命题中错误的是（　）．

A．若d＜0，则数列｛Sn｝有最大项

B．若数列｛Sn｝有最大项，则d＜0

C．若数列｛Sn｝是递增数列，则对任意n∈N＊均有Sn＞0

D．若对任意n∈N＊均有Sn＞0，则数列｛Sn｝是递增数列

解：由等差数列的求和公式可得

选项A，若d＜0，由二次函数的性质可得数列｛Sn｝有最大项，故正确．

选项B，若数列｛Sn｝有最大项，则对应的抛物线开口向下，则有d＜0，故正确．

选项C，若数列｛Sn｝是递增数列，则对应的抛物线开口向上，但不一定有任意n∈N＊，均有Sn＞0，故错误．

选项D，若对任意n∈N＊，均有Sn＞0，对应抛物线开口向上，d＞0，可得数列｛Sn｝是递增数列，故正确．(www.xing528.com)

故选C．

六、函数思想在立体几何中的应用

例题6 如图2所示，三棱锥P－ABC的高PO＝8，AC＝BC＝3，∠ACB＝30°，点M，N分别在BC和PO上，且CM＝x，PN＝2CM，则下面图中大致描绘了三棱锥N－AMC的体积V与x的变化关系（x∈（0，3］）的是（　）．

图2

解：由CM＝x，PN＝2CM，PO＝8，得NO＝8－2x．

所以VN－AMC表示的函数是开口向下的抛物线，故选A．

七、函数思想在解析几何中的应用

例题7 已知双曲线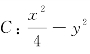＝1，P是C上的任意一点．

（1）求证：点P到双曲线C的两条渐近线的距离的乘积是一个常数；

（2）设点A的坐标为（3，0），求｜PA｜的最小值．

解：（1）设P（x1，y1）是双曲线上任意一点，

该双曲线的两条渐近线方程分别是x－2y＝0和x＋2y＝0．

所以点P到双曲线C的两条渐近线的距离的乘积是一个常数．

（2）设P的坐标为（x，y），则

因为｜x｜≥2，

所以当时，｜PA｜2的最小值为．

即｜PA｜的最小值为．

跟踪训练

1．设集合A＝｛x｜4x－2x＋2＋a＝0，x∈R｝．

（1）若A中仅有一个元素，求实数a的取值集合B；

（2）若对于任意a∈B，不等式x2－6x＜a（x－2）恒成立，求x的取值范围．

2．已知椭圆的中心在原点，对称轴在坐标轴上，直线y＝x＋1与该椭圆交于点P，Q且求椭圆的方程．

3．已知函数f（x）＝m·2x＋x2＋nx，记集合A＝｛x｜f（x）＝0，x∈R｝，集合B＝｛x｜f［f（x）］＝0，x∈R｝，若A＝B，且都不是空集，则m＋n的取值范围是（　）．

A．［0，4） B．［－1，4） C．［－3，5］ D．［0，7）

4．设函数f（x）＝ax2＋bx＋c（a＞0），且存在m，n∈R，使得［f（m）－m］2＋［f（n）－n］2＝0成立．

（1）若a＝1，当n－m＞1且t＜m时，试比较f（t）与m的大小；

（2）若直线x＝m，x＝n分别与f（x）的图像交于M，N两点，且M，N两点的连线被直线3（a2＋1）x＋（a2＋1）y＋1＝0平分，求出b的最大值．

（第6题）

5．已知函数等比数列｛an｝的前n项和为Sn＝f（n）－c，则an的最小值为_________．

6．如图所示，动点P在正方体ABCD－A1B1C1D1的对角线BD1上．过点P作垂直于平面BB1D1D的直线，与正方体表面相交于点M，N．设BP＝x，MN＝y，则函数y＝f（x）的图像大致是（　）．

（第7题）