知识结构
命题方向
解析几何的本质就是用代数的方法解决几何问题，解析几何中的问题多数是以直线与二次曲线为背景，考查二者之间的位置关系；处理的手段一般是“联立消元——判别式——根与系数的关系”．当问题涉及圆锥曲线上的点与焦点连线时，首先考虑运用定义．它可以很好地培养训练学生的分析问题、解决问题能力及逻辑推理能力与计算能力．因此成为高考考查的热点之一．
例题精讲
一、两条直线的位置关系
二、直线和圆的位置关系
例题2 设m，n∈R，若直线（m＋1）x＋（n＋1）y－2＝0与圆（x－1）2＋（y－1）2＝1相切，则m＋n的取值范围是（ ）．
解：由圆的方程（x－1）2＋（y－1）2＝1，得到圆心坐标为（1，1），半径r＝1．
三、弦长问题
例题3 已知曲线C：x2－y2＝1，过点T（t，0）作直线l和曲线C交于A、B两点．
（1）求曲线C的焦点到它的渐近线之间的距离．
（2）若t＝0，点A在第一象限，AH⊥x轴，垂足为H，连结BH，求直线BH倾斜角的取值范围．
（3）过点T作另一条直线m，m和曲线C交于E、F两点，问是否存在实数t，使得
和
同时成立？如果存在，求出满足条件的实数t的取值集合；如果不存在，请说明理由．
四、最值问题
例题4 已知点A（－2，0），B（2，0），动点M（x，y）满足直线AM与BM的斜率之积为
．记点M的轨迹为曲线C．
（1）求C的方程，并说明C是什么曲线．
（2）过坐标原点的直线交C于P，Q两点，点P在第一象限，PE⊥x轴，垂足为点E，连结QE并延长交C于点G．
（i）证明：△PQG是直角三角形；
（ii）求△PQG面积的最大值．
五、定点与定值问题
例题5 如图1，椭圆C：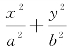
＝1（a＞b＞0）过点M（2，0），且右焦点为F（1，0），过F的直线l与椭圆C相交于A，B两点，设点P（4，3），记PA，PB的斜率分别为k1和k2．
图1
（1）求椭圆C的方程．
（2）如果直线l的斜率等于－1，求出k1·k2的值．
（3）探讨k1＋k2是否为定值？如果是，请求出该定值；如果不是，请求出k1＋k2的取值范围．
综上，k1＋k2是定值．
六、参数的取值范围
例题6 已知
．(www.xing528.com)
七、轨迹问题
例题7 已知抛物线C：y2＝2x的焦点为F，平行于x轴的两条直线l1、l2分别交C于A，B两点，交C的准线于P，Q两点．
（1）若点F在线段AB上，点R是PQ的中点，证明：AR∥FQ；
（2）若△PQF的面积是△ABF的面积的两倍，求AB中点的轨迹方程．
设满足条件的AB的中点为E（x，y）．
当AB与x轴不垂直时，由kAB＝kDE可得
而
＝y，所以y2＝x－1（x≠1）．
当AB与x轴垂直时，点E与D重合．
所以，所求轨迹方程为y2＝x－1．
八、自定义问题
跟踪训练
3．已知抛物线y2＝2px（p＞0），过动点M（a，0）且斜率为1的直线l与该抛物线交于不同的两点A，B．
（1）若｜AB｜≤2p，求a的取值范围；
（2）若线段AB的垂直平分线交AB于点Q，交x轴于点N，试求Rt△MNQ的面积．
4．如图，已知点F（1，0）为抛物线y2＝2px（p＞0），点F为焦点，过点F的直线交抛物线于A，B两点，点C在抛物线上，使得△ABC的重心G在x轴上，直线AC交x轴于点Q，且Q在点F右侧．记△AFG，△CQG的面积为S1，S2．
（1）求p的值及抛物线的准线方程；
（2）求
的最小值及此时点G的坐标．
（第4题）
（1）求C的方程；
（2）设直线l不经过P2点且与C相交于A，B两点，若直线P2A与直线P2B的斜率的和为－1，证明：直线l过定点．
6．已知椭圆C：
＋y2＝1的左、右焦点分别为点F1，F2，O为坐标原点．
（1）如图1，点M为椭圆C上的一点，N是MF1的中点，且NF2⊥MF1，求点M到y轴的距离；
（2）如图2，直线l：y＝kx＋m与椭圆C相交于P，Q两点，若在椭圆C上存在点R，使得四边形OPRQ为平行四边形，求实数m的取值范围．
（第6题）
7．已知曲线C是中心在原点，焦点在x轴上的双曲线的右支，它的右焦点为F（2，0），一条渐近线方程是
（1）求曲线C的方程；
（2）线段PQ是过曲线C右焦点F的一条弦，R是弦PQ的中点，当点P在曲线C上运动时，求点R到y轴距离的最小值．
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
