数学专题：函数的单调性、奇偶性、周期性

知识结构

命题方向

函数是贯穿高中数学的一根主线，函数的三性，即单调性、奇偶性、周期性，是函数概念的核心内容．其中尤以单调性最为重要，其题型多以幂、指、对为载体，同时也可以渗透到数学的其他部分，既有基础题，也有新颖独特的中档题和综合性的能力题．因此，在复习时不仅要熟练掌握其基础知识和基本性质，而且还要注意灵活运用．

例题精讲

一、奇偶性

例题1 已知函数f（x）＝x2＋（x≠0，常数a∈R）．

（1）讨论函数f（x）的奇偶性，并说明理由；

（2）若f（x）在x∈［2，＋∞）上是增函数，求a的取值范围．

解：（1）当a＝0时，f（x）＝x2，

对任意x∈（－∞，0）∪（0，＋∞），f（－x）＝（－x）2＝x2＝f（x），所以f（x）为偶函数．

当a≠0时，f（x）＝x2＋（a≠0，x≠0），

取x＝±1，得f（－1）＋f（1）＝2≠0，f（－1）－f（1）＝－2a≠0，

则f（－1）≠－f（1），f（－1）≠f（1），

所以，函数f（x）既不是奇函数，也不是偶函数．

（2）设2≤x1＜x2，则

要使函数f（x）在x∈［2，＋∞）上为增函数，必须f（x1）－f（x2）＜0恒成立．

而x1－x2＜0，x1x2＞4，即a＜x1x2（x1＋x2）恒成立．

又因为x1＋x2＞4，所以，x1x2（x1＋x2）＞16．所以，a的取值范围是（－∞，16］．

二、单调性

给定区间上的函数f（x），若对于任意的x1，x2∈D，当x1＜x2时，都有f（x1）＜f（x2）（f（x1）＞f（x2）），则称f（x）是区间D上的增（减）函数，D为其单调区间．

研究函数单调性的一般方法：一设，二作，三比较，即

①设x1＜x2∈D，②作差f（x1）－f（x2）并化简，③比较大小．

例题2 已知f（x）＝（2n－n2）x2n2＋3n－4（n∈N＊）在（0，＋∞）是增函数．

（1）求函数f（x）的解析式；

（2）设g（x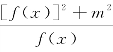）＝，讨论g（x）在（－∞，0）上的单调性，并求g（x）在区间（－∞，0）上的最小值．

由①得n＝1，此时f（x）＝x．

图1

②的解集为空集．

综上所述，f（x）＝x．

由于x1－x2＜0，x1x2＞0，若g（x1）－g（x2）＜0，则x1x2－m2＞0恒成立．

所以x1，x2∈（－∞，－｜m｜），因此，g（x）在（－∞，－｜m｜］上单调递增，在［－｜m｜，0）上单调递减，如图1所示．

所以，g（x）在（－∞，0）上的最大值为g（－｜m｜）＝－2｜m｜，无最小值．

三、函数的零点

函数F（x）＝f（x）－g（x）的零点就是方程f（x）＝g（x）的实数根，也就是函数y＝f（x）的图像与函数y＝g（x）的图像交点的横坐标，这个结论很有用．

图2

例题3 已知函数f（x）＋2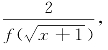＝当x∈（0，1］时，f（x）＝x2，若在区间（－1，1］内，g（x）＝f（x）－t（x＋1）有两个不同的零点，则实数t的取值范围是__________．

四、函数的最值

例题4 已知定义域为R的函数f（x）满足f（f（x）－x2＋x）＝f（x）－x2＋x．

（1）若f（2）＝3，求f（1）；又若f（0）＝a，求f（a）．

（2）设有且仅有一个实数x0，使得f（x0）＝x0，求函数f（x）的解析式．

（3）在（2）的条件下，求f（x）在区间［0，m］上的最大值和最小值．

解：（1）因为对任意x∈R，有f（f（x）－x2＋x）＝f（x）－x2＋x，所以f（f（2）－22＋2）＝f（2）－22＋2．

又由f（2）＝3，得f（3－22＋2）＝3－22＋2，即f（1）＝1．(www.xing528.com)

若f（0）＝a，即f（a－02＋0）＝a－02＋0，即f（a）＝a．

（2）已知对任意x∈R，有f（f（x）－x2＋x）＝f（x）－x2＋x，因为有且只有一个实数x0，使得f（x0）＝x0，所以对任意x∈R，有f（x）－x2＋x＝x0．

在上式中令x＝x0，f（x0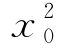）－＋x0＝x0，

又因为f（x0）＝x0，则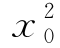－x0＝0，所以x0＝0或1．

若x0＝0，即f（x）－x2＋x＝0，即f（x）＝x2－x，但方程x2－x＝x0有两个不同实根，与题设条件矛盾，故x0≠0；

若x0＝1，则有f（x）－x2＋x＝1，即f（x）＝x2－x＋1，易验证该函数满足题设条件．

综上，所求函数为f（x）＝x2－x＋1．

（3）由于f（x）＝x2－x＋1，对称轴为，

五、反函数

例题5 已知函数f（x）＝log2．

（1）求函数f（x）的定义域；

（2）若函数f（x）的定义域关于坐标原点对称，试讨论它的奇偶性和单调性；

（3）在（2）的条件下，记f－1（x）为f（x）的反函数，若关于x的方程f－1（x）＝5k·2x－5k有解，求k的取值范围．

而（x1＋5）（x2－5）－（x1－5）（x2＋5）＝10（x2－x1）＞0，

所以f（x1）－f（x2）＞0，所以f（x）在（5，＋∞）内单调递减．

由于f（x）为奇函数，所以在（－∞，－5）内单调递减．

六、周期性

由于函数f（x）的最小正周期为2且为奇函数，则f（1）＝f（－1）＝－f（1），所以f（1）＝0，f（－1）＝0．

又因为f（x）是R上的奇函数，所以f（0）＝0．

跟踪训练

1．已知函数f（x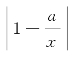）＝（x≠0，常数a∈R）．

（1）讨论函数f（x）的奇偶性，并说明理由；

（2）当a＞0时，研究函数f（x）在x∈（0，＋∞）内的单调性．

2．已知函数f（x）＝a·2x＋b·3x，其中常数a，b满足ab≠0．

（1）若ab＞0时，判断函数f（x）的单调性；

（2）若ab＜0时，求f（x＋1）＞f（x）的取值范围．

3．在区间D上，如果函数f（x）为减函数，而xf（x）为增函数，则称f（x）为D上的弱减函数．若．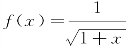

（1）判断f（x）在区间［0，＋∞）上是否为弱减函数；

（2）当x∈［1，3］时，不等式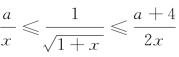恒成立，求实数a的取值范围；

（3）若函数g（x）＝f（x）＋k｜x｜－1在［0，3］上有两个不同的零点，求实数k的取值范围．

4．已知a∈R，函数．

（1）当a＝5时，解不等式f（x）＞0；

（2）若关于x的方程f（x）－log2［（a－4）x＋2a－5］＝0的解集中恰好有一个元素，求a的取值范围；

（3）设a＞0，若对任意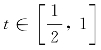，函数f（x）在区间［t，t＋1］上的最大值与最小值的差不超过1，求a的取值范围．

5．已知函数y＝f（x）的反函数为y＝f－1（x）．定义：若对给定的实数a（a≠0），函数y＝f（x＋a）与y＝f－1（x＋a）互为反函数，则称y＝f（x）满足“a和性质”．

（1）判断函数g（x）＝x2＋1（x＞0）是否满足“1和性质”，并说明理由；

（2）求所有满足“2和性质”的一次函数．

6．我们把定义在R上，且满足f（x＋T）＝af（x）（其中常数a，T满足a≠1，a≠0，T≠0）的函数叫做似周期函数．

（1）若某个似周期函数y＝f（x）满足T＝1且图像关于直线x＝1对称．求证：函数f（x）是偶函数；

（2）当T＝1，a＝2时，某个似周期函数在0≤x＜1时的解析式为f（x）＝x（1－x），求函数y＝f（x），x∈［n，n＋1），n∈Z的解析式；

（3）对于确定的T＞0且0＜x≤T时，f（x）＝3x，试研究似周期函数y＝f（x）在区间（0，＋∞）上是否可能是单调函数？若可能，求出a的取值范围；若不可能，请说明理由．