知识结构
命题方向
不等式是高中数学的主要工具之一，因此是高考的热点之一．在高考试题中既有基础题又有综合题，主要渗透在代数、几何、三角的解答题中．而线性规划问题，一般地，是以不等式为载体求目标函数的最值，大多是以小题出现，因此，在复习时要对其难易度做好调控．
例题精讲
一、不等式的性质
例题1 若a＞b＞0，c＜d＜0，则一定有（ ）．
A．ad＞bc B．ad＜bc C．ac＞bd D．ac＜bd
解：因为c＜d＜0，所以－c＞－d＞0．
又a＞b＞0，则一定有－ac＞－bd，可得ac＜bd．故选D．
二、不等式的解法
三、基本不等式
例题5 若实数x，y，m满足｜x－m｜＞｜y－m｜，则称x比y远离m．
（1）若x2－1比1远离0，求x的取值范围；
（2）对任意两个不相等的正数a，b，证明：a3＋b3比a2b＋ab2远离
解：（1）因为｜x2－1｜＞1，所以x2－1＞1或x2－1＜－1（舍去）．
四、不等式的应用
例题6 为了保护环境，造福人类，某县环保部门拟建一座底面积为200m2的长方体二级净水处理池（如图1），池深度一定，池的外壁建造单价为400元／m2，中间一条隔墙建造单价为100元／m2，池底建造单价为60元／m2．
图1(www.xing528.com)
（1）一般情况下，净水处理池的长设计为多少m时，可使总造价最低？
（2）若受地形限制，净水处理池的长、宽都不能超过14．5m，那么此时净水池的设计为多少m时，可使总造价最低？
解：（1）设净水池长为x m，高为h m，则宽为
m，则总造价
故当净水池的长设计为15m时，总造价最低．
图2
五、线性规划
跟踪训练
1．已知a，b，c，d均为实数，下列命题中，正确的个数是（ ）．
A．0 B．1 C．2 D．3
2．若不等式ax2＋bx＋c＞0的解集为｛x｜α＜x＜β｝（0＜α＜β），且ac≠0，求不等式cx2＋bx＋a＜0的解集．
3．若不等式｜x－4｜－｜x－3｜≤a对一切x∈R恒成立，则实数a的取值范围是___________．
4．解关于x的不等式：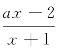
＞1（a≤1）．
5．若实数a，b＞0，满足abc＝a＋b＋c，a2＋b2＝1，则实数c的最小值为______．
6．某地区上年度电价为0．8元／（kW·h），年用电量为a（kW·h），本年度计划将电价降到0．55元／（kW·h）至0．75元／（kW·h）之间，而用户期望电价为0．4元／（kW·h），经测算，下调电价后
的用电量与实际电价和用户期望电价的差成反比（比例系数为k），该地区的电力成本为0．3元／（kW·h）．
（1）写出本年度电价下调后，电力部门的收益y与实际电价x的函数关系；
（2）设k＝0．2a，当电价最低定为多少时仍可保证电力部门的收益比上一年至少增长20%？
［注：收益＝实际用电量×（实际电价—成本）］
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
