上海新高考·数学专题1集合与命题攻略

知识结构

命题方向

在高考中，对集合的考查主要集中在以下两个方面：一是考查考生对集合概念的理解与基础知识的掌握；二是考查与其他知识点的综合运用能力。而对于命题这一知识点主要考查基本概念的理解以及四种命题间的关系．

例题精讲

一、元素与集合的关系

例题1 设非空集合S＝｛x｜m≤x≤l｝，满足当x∈S时，有x2∈S．给出如下三个命题：①若m＝1，则S＝｛1｝； ②若m＝－，则≤l≤1； ③若l＝，则－≤m≤0．

其中正确的命题的个数是（　）．

A．0 B．1 C．2 D．3

解：①当m＝1时，S＝｛x｜1≤x≤l｝，若l＞1，则l2＞l，从而l2∉S，与已知矛盾，所以l＝1，即S＝｛1｝，因此，①正确．

二、集合的运算

例题2 设集合A＝｛a1，a2，a3，a4｝，B＝，其中a1，a2，a3，a4都是正整数，且a1＜a2＜a3＜a4．

（1）若A∩B＝｛a1，a4｝，且a1＋a4＝10，试求a1，a4的值；

（2）若A∪B的元素的和为124，在（1）的条件下求A，B．

解：（1）由于A∩B＝｛a1，a4｝，a1＜a2＜a3＜a4∈N＊，

则a1＝，所以a1＝1，a4＝9．

（2）由（1）得A＝｛1，a2，a3，9｝，B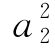＝｛1，，，81｝．

若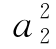＝9，则a2＝3，1＋3＋9＋a3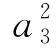＋＋81＝124，

即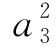＋a3－30＝0，

解得a3＝5或a3＝－6（舍）．

此时A＝｛1，3，5，9｝，B＝｛1，9，25，81｝．

若＝9，则a3＝3，从而a2＝2，从而1＋2＋3＋9＋4＋81＝100≠124，矛盾．

因此A＝｛1，3，5，9｝，B＝｛1，9，25，81｝．

三、充分必要条件

例题3 判断下列命题的真假：

（1）x∈A∩B，当且仅当x∈A且x∈B；

（2）x∈Z或x∈Q是x∈R的充分不必要条件；

（3）若α，β为锐角，则α＋β＝90°是sinα＝cosβ的充要条件；

（4）a，b，c成等比数列的充要条件是；

（5）函数f（x）＝｜x－a｜在区间［1，＋∞）上为增函数的必要不充分条件是a＝1．

解：（1）根据交集的定义可知，该命题为真命题．

（2）x∈Z或x∈Q，即x∈Q，QR，故该命题为真命题．

（3）由于α，β为锐角，α＋β＝90°，则sinα＝sin（90°－β）＝cosβ．

反过来，sinα＝cosβ＝sin（90°－β），

又0°＜β＜90°，则0°＜90°－β＜90°，

而0°＜α＜90°，则α＝90°－β，(www.xing528.com)

所以α＋β＝90°．故该命题为真命题．

（4）由于a，b，c成等比数列，则b2＝ac，即b＝±取b＝0，a＝0，c＝1，满足但a，b，c不成等比数列．故该命题为假命题．

（5）f（x）＝｜x－a｜在［a，＋∞）上为增函数，当a≤1时，f（x）在［1，＋∞）上为增函数，当a＞1时，f（x）在［1，＋∞）上不是增函数，故a＝1是f（x）＝｜x－a｜在［1，＋∞）上为增函数的充分不必要条件，故该命题为假命题．

四、命题

例题4 已知p：方程x2＋mx＋1＝0有两个不等的负根；命题q：方程4x2＋4（m－2）x＋1＝0无实根．若“p或q”为真，“p且q”为假，求m的取值范围．

解：若方程x2＋mx＋1＝0有两个不等的负根，则解得m＞2，

即命题p：m＞2．

若方程4x2＋4（m－2）x＋1＝0无实根，则Δ＝16（m－2）2－16＝16（m2－4 m＋3）＜0，解得1＜m＜3，即q：1＜m＜3．

因为“p或q”为真，所以p，q至少有一个为真．

又“p且q”为假，所以命题p，q至少有一个为假，

因此，命题p，q应一真一假，即命题p为真，命题q为假或命题p为假，命题q为真．

所以或解得m≥3或1＜m≤2．

五、综合提升

例题5 从集合U＝｛a，b，c，d｝的子集中选出4个不同的子集，需同时满足以下两个条件：

①Ø，U都要选出；

②对选出的任意两个子集A和B，必有A⊆B或B⊆A，那么共有________种不同的选法．

解：由于Ø，U都要选出，所以只需再选出两个不同的子集即可，①若其中一个子集只含一个元素，另一个子集含两个元素，则有×＝12（种）不同的选法；②若其中一个子集只含一个元素，另一个子集含三个元素，则有×＝12（种）不同的选法；③若其中一个子集含两个元素，另一子集含三个元素，则有×＝12（种）不同的选法．所以共有12＋12＋12＝36（种）不同的选法．

跟踪训练

1．已知实数集A满足：若x∈A，且x≠±1，0，则∈A．

（1）求证：当2∈A时，A中还有3个元素；

（2）设2020∈A，求出集合A中的其他元素；

（3）请你根据（1）（2）作出正确猜想，并加以证明．

2．已知集合A＝｛x｜x2＋（a－1）x－a＞0｝，B＝｛x｜（x＋a）（x＋b）＞0｝，其中a≠b，M＝｛x｜x2－2x－3≤0｝，全集为U＝R．

（1）若∁UB＝M，求a，b的值；

（2）若a＞b＞－1，求A∩B；

（3）若a2＋∈∁UA，求a的取值范围．

3．已知数列｛an｝的前n项和Sn＝pn＋k（p≠0，p≠1），求数列｛an｝是等比数列的充要条件．

4．已知全集U＝R，非空集合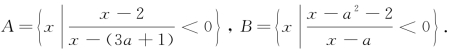

（1）当a＝时，求（∁UB）∩A；

（2）命题p：x∈A，命题q：x∈B，若q是p的必要条件，求实数a的取值范围．

5．设n为正整数，集合A＝｛α｜α＝（t1，t2，…，tn），tk∈｛0，1｝，k＝1，2，…，n｝．对于集合A中的任意元素α＝（x1，x2，…，xn）和β＝（y1，y2，…，yn），记

（1）当n＝3时，若α＝（1，1，0），β＝（0，1，1），求M（α，α）与M（α，β）的值；

（2）当n＝4时，设B是A的子集，且满足：对于B中的任意元素α，β，当α，β相同时，M（α，β）是奇数；当α，β不同时，M（α，β）是偶数．求集合B中元素个数的最大值；

（3）给定不小于2的n，设B是A的子集，且满足：对于B中的任意两个不同的元素α，β，M（α，β）＝0．写出一个集合B，使其元素个数最多，并说明理由．