测定季节变动的方法与统计学原理

通过掌握现象的季节变动规律，可以为决策和预测提供重要依据；从原序列中剔除季节变动的影响，能够更好地分析其他因素。在乘法模型中，季节变动的测定和分离都通过季节指数实现。首先按是否消除长期趋势影响来分，测定方法可分为两大类：

一是不考虑长期趋势的影响，直接根据原序列去测定，常用方法是同期平均法；

二是先剔除长期趋势，然后根据趋势剔除后的序列来测定，常用方法是移动平均趋势剔除法。

要测定季节变动，至少要有三个以上季节周期的数据。如果季节变动的规律性不是很稳定，则所需要的数据还应更多一些为好。

（一）同期平均法

1.基本原理

假定时间序列呈水平趋势，通过对多年同期的数据进行简单算术平均，以消除不规则变动，再将各季节水平（同期平均数）与水平趋势值对比，即可得到季节指数。

2.计算步骤

（1）计算同期平均数（i=1，2，…，L）

将不同年份同一季节的多个数据进行简单算术平均。其目的是消除不规则变动的影响。一般要先将各年同一季节的数据对齐排列。

（2）计算全部数据的总平均数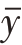

代表消除了季节变动和不规则变动之后的全年平均水平，亦即整个时间序列的水平趋势值。

（3）计算季节指数（也称为季节比率）Si。

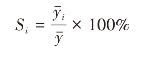
注意：

Si＞100%，表示现象在第i期处于旺季，即第i期水平高于全年平均水平；

Si＜100%，表示第i期是个淡季，即该季节的水平低于全年平均水平。

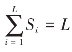在一个完整的季节周期中，季节指数的总和等于季节周期的时间项数，或季节指数的均值等于1。

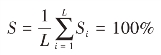
否则就要进行调整（即归一化处理）。调整方法是用各项季节指数除以全部季节指数的均值（或将所求的各项季节指数都乘以一个调整系数即可）。

【例7-7】企业生产的一种学生学习用复读机的销售量数据如表7-7所示，试用同期平均法计算各月的季节指数。(www.xing528.com)

表7-7　学习复读机销售量

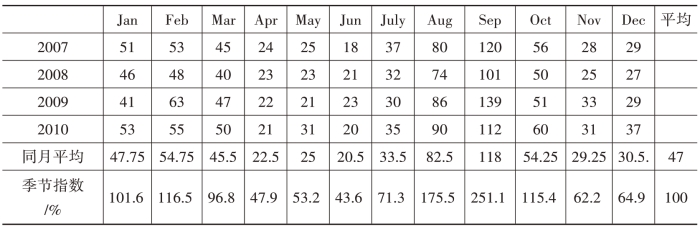
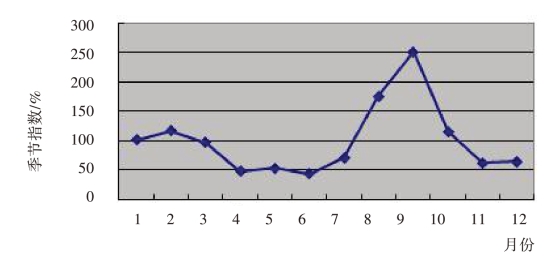
图7-1　季节指数

同期平均法简单，易理解，但只适用于呈水平趋势的序列。当现象呈现出明显上升（下降）趋势时，总会高估（低估）年末季节指数，相应地低估（高估）年初季节指数。

（二）移动平均趋势剔除法

1.趋势剔除法的基本原理

首先测定出各期趋势值，然后从原序列中消除趋势成分，最后再通过平均的方法消除不规则变动，从而测定出季节变动程度。最常用的趋势剔除法是移动平均趋势剔除法。采用移动平均法测定长期趋势，剔除趋势后再计算季节指数。实质上，此方法也适用于包含循环变动的场合。

2.移动平均趋势剔除法的步骤

（1）计算移动平均值（M）

对原序列计算平均项数等于季节周期L的中心化移动平均值，旨在消除原序列中的季节变动S和不规则变动I。若序列不包含循环变动，即Y=T·S·I，则M=T。假定时间序列也包含循环变动，即Y=T·S·C·I，则M=T·C，可称之为趋势-循环值。

（2）剔除原序列中的趋势成分（或趋势-循环成分），得到只含季节变动和不规则变动的比率序列即：

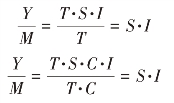
（3）消除不规则变动I

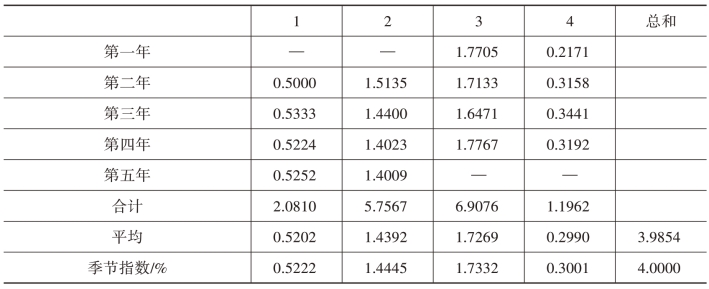
将各年同期（同月或同季）的比率（S·I）进行简单算术平均，可消除不规则变动I，从而可得到季节指数S。

（4）调整季节指数

对所求季节指数进行归一化处理。

【例7-8】

表7-8　某企业五年销售额

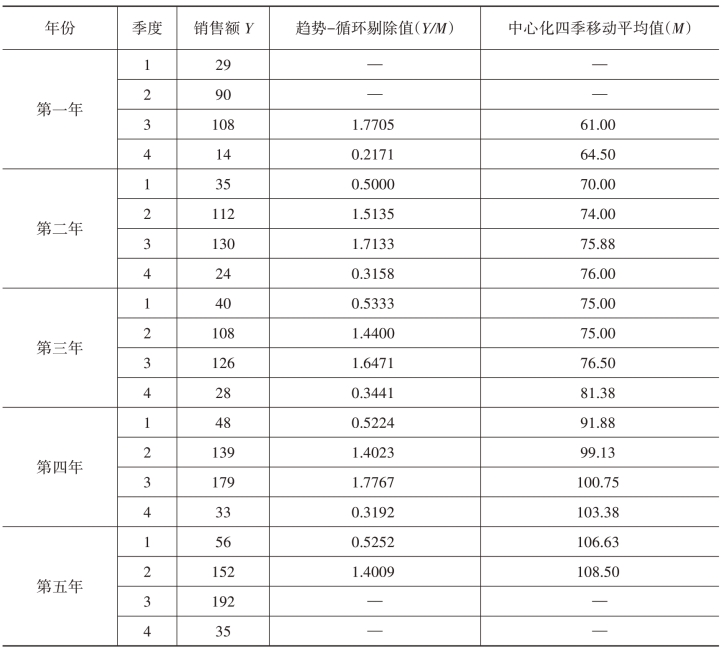
表7-9　季节指数的计算表