(一)发展速度=报告期水平/基期水平
说明:现象在观察期内发展变化的相对程度;有环比发展速度与定基发展速度之分。
1.环比发展速度=报告期水平/上期水平=yi/yi-1
反映现象逐期发展变动的程度,也可称为逐期发展速度。
2.定基发展速度=报告期水平/固定基期水平=yt/y0
反映现象在较长一段时间内总的发展变动程度,也称为发展总速度。
3.二者关系:
定基发展速度=相应时期的环比发展速度之积。
相邻两定基发展速度之商=相应的环比发展速度。
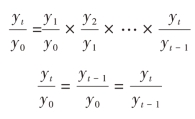
为了消除季节变动因素的影响,可计算:
同比发展速度=
(二)增长速度(增长率)
1.增长速度(增减速度)——增长量与基期水平之比,说明现象增长变化的相对程度:
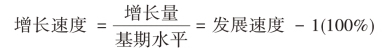
2.基期不同,分环比增长速度与定基增长速度

3.二者关系
定基增长速度(总增长速度)不等于相应各环比增长速度之和(积)。
4.几种速度指标之间的相互关系

5.为了消除季节变动因素的影响,也常常计算同比增长速度:

6.速度的表现形式和文字表述
(1)速度指标的表现形式:一般为%、倍数,也有用‰、番数等等。
翻m番,则有:报告期水平=基期水平×2m
(2)速度的文字表述:
①发展速度——相当于、发展为、增长到、减少到、下降为…
报告期水平增长为基期水平的…%;
以基期水平为100%,报告期水平增长为…%.
②增长速度——提高(了)、减少(了)、下降(了)…
报告期水平比基期水平增长(了)…%;
以基期水平为100%,报告期水平增长(了)…%。
(三)平均发展速度和平均增长速度(https://www.xing528.com)
1.概念
平均增长速度——表示逐期增长变动的平均程度,即各期环比增长速度的一般水平,但不能对各环比增长速度直接平均。因为算术平均法或几何平均法都不符合增长速度这种现象的性质。平均增长速度为正(负)值,表明平均说来现象在考察期内逐期递增(减)。
正确的计算方法:平均增长速度=平均发展速度-1
2.几何平均法计算平均发展速度(水平法)
以xi表示环比发展速度,根据环比发展速度与总速度的关系,计算平均发展速度可以采用几何平均法,以下三个计算公式实质上是一致的。可根据所掌握的数据来选择。

【例7-6】根据表7-3的数据,计算中国2011—2018年居民消费水平的平均发展速度和平均增长速度。
解:平均发展速度可根据三种资料来计算:

平均增长速度=110.9%-100%=10.9%
即2011—2018年间,我国居民消费水平平均每年递增10.9%。
(1)几何平均法的特点
①用所求平均发展速度代表各环比发展速度,推算的最末一期的水平与实际相等,推算的总速度(最末一期的定基速度)也与实际相等。
②几何平均法计算平均发展速度着眼于最末一期的水平,故称为“水平法”。如果关心现象在最后一期应达到的水平时,采用水平法计算平均发展速度比较合适。
③几何平均法较为简单直观,既便于各种速度之间的推算,也便于预测未来某期的水平,因此有着广泛的应用。
(2)平均发展速度的应用
①根据平均速度预测现象经过一段时间以后可能达到的水平。
![]()
②例如,若我国居民人均消费水平继续按上面所求出的平均速度递增,则可预测到2015年,居民人均消费水平可达:9963×(1.1159)5=17239.17(元)
③利用平均发展速度的原理,还可在年度增长率zy与月增长率zm(季增长率zs)之间进行换算。它们的关系可表示为:
![]()
例如,某地区居民消费总额2016年9月为200亿元,2018年5月为260亿元。则居民民消费总额的月平均增长率和年平均增长率分别为:
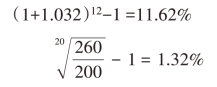
3.方程式法计算平均发展速度
(1)已知:各期实际水平的总和为:

若将各期水平yi用期初水平与各期环比发展速度xi的乘积来表示,则上式可变成为:
![]()
假设以平均发展速度作为各环比发展速度的代表值,用它来推算各期水平,并能使所推算的各期水平总和与实际相等,则有:

解上述方程,其正根=平均发展速度。
(2)方程式法计算平均发展速度的特点
方程式法计算结果取决于考察期内各期实际水平的累计总和,所以计算平均发展速度的方程式法又称为“累计法”。以所求平均发展速度代替各期环比发展速度,推算的考察期内各期水平的累计总和与实际相等。着眼于考察全期的累计水平时,就适合用方程式法来计算平均发展速度。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




