一元线性回归模型检验-《统计学原理》

（一）回归模型检验的种类

回归模型的检验包括理论意义检验、一级检验和二级检验。

理论意义检验主要涉及参数估计值的符号和取值区间，如果它们与实质性科学的理论以及人们的实践经验不相符，就说明模型不能很好地解释现实的现象。例如，在前面所举的消费函数中，β2的取值区间应在0至1之间。在对实际的社会经济现象进行回归分析时，常常会遇到经济意义检验不能通过的情况。造成这一结果的主要原因是：社会经济的统计数据无法像自然科学中的统计数据那样通过有控制的实验去取得，因而所观测的样本容量有可能偏小，不具有足够的代表性，或者不能满足标准线性回归分析所要求的假定条件。

一级检验又称统计学检验，它是利用统计学中的抽样理论来检验样本回归方程的可靠性，具体又可分为拟合程度评价和显著性检验。一级检验是对所有现象进行回归分析时都必须通过的检验。

二级检验又称经济计量学检验，它是对标准线性回归模型的假定条件能否得到满足进行检验，具体包括序列相关检验、异方差性检验、多重共线性检验等。二级检验对于社会经济现象的定量分析具有特别重要的意义。

（二）拟合程度评价

因变量y的取值是不同的，y取值的这种波动称为变差。变差来源于两个方面：一是由于自变量x的取值不同造成的；二是除x以外的其他因素（如x对y的非线性影响、测量误差等）的影响。对一个具体的观测值来说，变差的大小可以通过该实际观测值与其均值之差y-来表示。

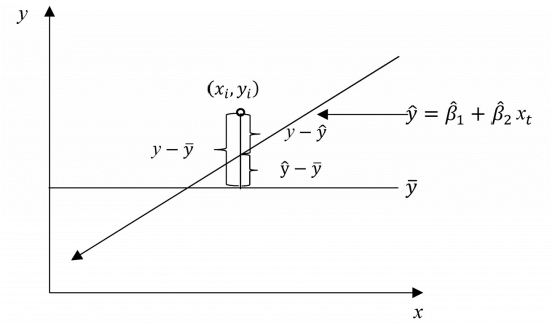
图6-8　拟合程度评价

上式中，SST是总离差平方和；SSR是由回归直线可以解释的那一部分离差平方和，称为回归平方和；SSE是用回归直线无法解释的离差平方和，称为残差平方和。式子两边同除以SST，得：

显而易见，各个样本观测点与样本回归直线靠得越紧，SSR在SST中所占的比例就越大。因此，可定义这一比例为决定系数r2，即有：

决定系数是对回归模型拟合程度的综合度量，决定系数越大，模型拟合程度越高。决定系数越小，则模型对样本的拟合程度越差。

决定系数r2具有如下特性：

1.决定系数r2具有非负性。由决定系数的定义式可知，r2的分子、分母均是不可能为负值的平方和，因此其比值必大于零。（但是在回归模型中不包括截距项的场合，由于总离差平方和的分解公式不成立，按该式计算的r2有可能小于0。）

2.决定系数的取值范围为0≤r2≤1。

3.决定系数是样本观测值的函数，它也是一个统计量。

4.在一元线性回归模型中，决定系数是单相关系数的平方。

【例6-7】利用例6-5中的数据，计算例6-5所拟合的样本回归方程的决定系数。(www.xing528.com)

解：

上式中的SST是利用例6-5表中给出的数据按下式计算的：

（三）显著性检验

回归分析中的显著性检验包括两方面的内容：一是对各回归系数的显著性检验；二是对整个回归方程的显著性检验。在一元线性回归模型中，由于只有一个解释变量X，对β2=0的检验与对整个方程的显著性检验是等价的。

所谓回归系数的显著性检验，就是根据样本估计的结果对总体回归系数的有关假设进行检验。β1与β2的检验方法是相同的，但β2的检验更为重要，因为它表明自变量对因变量影响的程度。

1.t检验

（1）提出假设。对回归系数进行显著性检验，所提出的假设的一般形式是：

式中，H0表示原假设；H1表示备择假设；β*2是假设的总体回归系数的真值。在许多回归分析的计算机程序里，常常令β*2=0。这是因为β2是否为0，可以表明X对Y是否有显著的影响。

（2）确定显著水平a。显著水平的大小应根据犯哪一类错误可能带来损失的大小确定。一般情况下可取0.05。

（3）计算回归系数的t值。

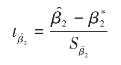
（4）确定临界值。

t检验的临界值是由显著水平和自由度决定的。这时应该注意，原假设和备择假设设定的方式不同，据以判断的接受域和拒绝域也不相同。对此，在双侧检验的场合，依据a和df，查t分布表所确定的临界值是（-ta/2）和（ta/2）；而在单侧检验的场合，所确定的临界值是（ta）。

（5）做出判断。

如果的绝对值大于临界值的绝对值，就拒绝原假设，接受备择假设；反之，如果的绝对值小于临界值的绝对值，则接受原假设。

2.p检验

回归系数的显著性检验还可以采用p检验。其前三步与t检验相同，但t值计算出来之后，并不与t分布的临界值进行对比，而是直接计算自由度为n-2的t统计量大于或小于根据样本观测值计算的的概率（即p值）。然后将其与给定的显著水平a对比，如果p小于a，则拒绝原假设，反之则接受原假设。